Livermore Model

The class G4LivermoreBremsstrahlungModel calculates the continuous energy loss due to low energy gamma emission and simulates the gamma production by electrons. The gamma production threshold for a given material \(\omega_c\) is used to separate the continuous and the discrete parts of the process. The energy loss of an electron with the incident energy \(T\) are expressed via the integrand over energy of the gammas:

\[{dE\over dx}=\sigma(T){{\int^{\omega_c}_{0.1eV}t{d\sigma\over d\omega}d\omega} \over{\int^{T}_{0.1eV} {d\sigma\over d\omega}d\omega}},\]

where \(\sigma(T)\) is the total cross-section at a given incident kinetic energy, \(T\), 0.1 eV is the low energy limit of the EEDL data. The production cross-section is a complementary function:

\[\sigma=\sigma(T){{\int^{T}_{\omega_c}{d\sigma\over d\omega}d\omega}\over {\int^{T}_{0.1eV}{d\sigma\over d\omega}d\omega}}.\]

The total cross-section, \(\sigma_s\), is obtained from an interpolation of the evaluated cross-section data in the EEDL library [STPerkins89].

The EEDL data [eal99] of total cross-sections are parametrised [STPerkins89] according to (1). The probability of the emission of a photon with energy, \(\omega\), considering an electron of incident kinetic energy, \(T\), is generated according to the formula:

\[{d\sigma \over d\omega} = {F(x) \over x}, \;\; \mbox{with} \;\; x = {\omega \over T}.\]

The function, \(F(x)\), describing energy spectra of the outgoing photons is taken from the EEDL library. For each element 15 points in \(x\) from 0.01 to 1 are used for the linear interpolation of this function. The function \(F\) is normalised by the condition \(F(0.01) = 1\). The energy distributions of the emitted photons available in the EEDL library are for only a few incident electron energies (about 10 energy points between 10 eV and 100 GeV). For other energies a logarithmic interpolation formula (1) is used to obtain values for the function, \(F(x)\). For high energies, the spectral function is very close to:

\[F(x) = 1 - x + 0.75x^2.\]

Bremsstrahlung angular distributions

The angular distribution of the emitted photons with respect to the incident electron can be sampled according to three alternative generators described below. The direction of the outgoing electron is determined from the energy-momentum balance. This generators are currently implemented in G4ModifiedTsai, G4Generator2BS and G4Generator2BN classes.

G4ModifiedTsai

The angular distribution of the emitted photons is obtained from a simplified [eal93] formula based on the Tsai cross-section [Tsa74, Tsa77], which is expected to become isotropic in the low energy limit.

G4Generator2BS

In G4Generator2BS generator, the angular distribution of the emitted photons is obtained from the 2BS Koch and Motz bremsstrahlung double differential cross-section [KM59]:

\[d\sigma_k,_\theta = \frac{4Z^2 r_0^2}{137} \frac{dk}{k} ydy \left\{ \frac{16y^2E}{(y^2+1)^4E_0}- \frac{(E_0+E)^2}{(y^2+1)^2E_0^2} + \left[ \frac{E_0^2+E^2}{(y^2+1)^2E_0^2}- \frac{4y^2E}{(y^2+1)^4E_0}\right]\ln M(y)\right\}\]

where \(k\) the photon energy, \(\theta\) the emission angle, \(E_0\) and \(E\) are the initial and final electron energy in units of \(m_e c^2\), \(r_0\) is the classical electron radius and \(Z\) the atomic number of the material. \(y\) and \(M(y)\) are defined as:

\[\begin{split}y &= E_0\theta \\ \frac{1}{M(y)} &= \left(\frac{k}{2E_0E}\right)^2+\left(\frac{Z^{1/3}}{111(y^2+1)}\right)^2\end{split}\]

The adopted sampling algorithm is based on the sampling scheme developed by A. F. Bielajew et al. [AFBC89], and later implemented in EGS4. In this sampling algorithm only the angular part of 2BS is used, with the emitted photon energy, \(k\), determined by Geant4 \(d\sigma/dk)\) differential cross-section.

G4Generator2BN

The angular distribution of the emitted photons is obtained from the 2BN Koch and Motz bremsstrahlung double differential cross-section [KM59] that can be written as:

\[\begin{split}d\sigma_{k, \theta} & = \frac{Z^2 r_0^2}{8\pi 137}\frac{dk}{k} \frac{p}{p_0} d\Omega_k \left \{ \frac{8\sin^2\theta (2E_0^2+1)}{p_0^2\Delta_0^4}- \right.{} \\ & \left. \frac{2(5E_0^2+2EE_0+3)}{p_0^2\Delta_0^2} - \frac{2(p_0^2-k^2)}{Q^2\Delta_0} + \frac{4E}{p_0^2\Delta_0} + \frac{L}{pp_0} \right.{} \\ & \left. \left[ \frac{4E_0\sin^2\theta(3k-p_0^2E)}{p_0^2\Delta_0^4} + \frac{4E_0^2(E_0^2+E^2)} {p_0^2\Delta_0^2} + \right. \right.{} \\ & \left.\left. \frac{2-2(7E_0^2-3EE_0+E^2)}{p_0^2\Delta_0^2} + \frac{2k(E_0^2+EE_0-1)} {p_0^2\Delta_0} \right] \right.{} \\ & \left. -\left( \frac{4\epsilon}{p\Delta_0} \right) + \left( \frac{\epsilon^Q}{pQ} \right) \left[ \frac{4}{\Delta^2_0} - \frac{6k}{\Delta_0} - \frac{2k(p_0^2-k^2)}{Q^2\Delta_0} \right] \right \}\end{split}\]

in which:

\[\begin{split}L &= \ln\left[\frac{EE_0-1+pp_0}{EE_0-1-pp_0}\right] \\ \Delta_0 &= E_0-p_0\cos\theta \\ Q^2 &= p_0^2+k^2-2p_0k\cos\theta \\ \epsilon &= \ln\left[\frac{E+p}{E-p}\right] \qquad \epsilon^Q=\ln\left[\frac{Q+p}{Q-p}\right]\end{split}\]

where \(k\) is the photon energy, \(\theta\) the emission angle and \((E_0,p_0)\) and \((E,p)\) are the total (energy, momentum) of the electron before and after the radiative emission, all in units of \(m_e c^2\).

Since the 2BN cross–section is a 2-dimensional non-factorized distribution an acceptance-rejection technique was the adopted. For the 2BN distribution, two functions \(g_1(k)\) and \(g_2(\theta)\) were defined:

\[g_1(k) = k^{-b} \qquad\qquad g_2(\theta)=\frac{\theta}{1+c\theta^2}\]

such that:

\[Ag_1(k)g_2(\theta) \ge \frac{d\sigma}{dkd\theta}\]

where A is a global constant to be completed. Both functions have an analytical integral \(G\) and an analytical inverse \(G^{-1}\). The \(b\) parameter of \(g_1(k)\) was empirically tuned and set to \(1.2\). For positive \(\theta\) values, \(g_2(\theta)\) has a maximum at \(1/\sqrt(c)\). \(c\) parameter controls the function global shape and it was used to tune \(g_2(\theta)\) according to the electron kinetic energy.

To generate photon energy \(k\) according to \(g_1\) and \(\theta\) according to \(g_2\) the inverse-transform method was used. The integration of these functions gives

\[G_1 = C_1 \int_{k_{min}}^{k_{max}} k'^{-b}dk' = C_1 \frac{k^{1-b}-k^{1-b}_{min}}{1-b}\]

\[G_2 = C_2 \int_{0}^{\theta} \frac{\theta'}{1+c\theta'^2}d\theta'=C_2 \frac{\log(1+c\theta^2)}{2c}\]

where \(C_1\) and \(C_2\) are two global constants chosen to normalize the integral in the overall range to the unit. The photon momentum \(k\) will range from a minimum cut value \(k_{min}\) (required to avoid infrared divergence) to a maximum value equal to the electron kinetic energy \(E_k\), while the polar angle ranges from 0 to \(\pi\), resulting for \(C_1\) and \(C_2\):

\[C_1 = \frac{1-b}{E_k^{1-b}} \qquad\qquad C_2 = \frac{2c}{\log(1+c\pi^2)}\]

\(k\) and \(\theta\) are then sampled according to:

\[k = \left[ \frac{1-b}{C_1}\xi_1 + k_{min}^{1-b} \right] \qquad\qquad \theta = \sqrt{\frac{\exp\left(\frac{2c\xi_2}{C_1}\right)}{2c}}\]

where \(\xi_1\) and \(\xi_2\) are uniformly sampled in the interval (0,1). The event is accepted if:

\[uAg_1(k)g_2(\theta) \le \frac{d\sigma}{dkd\theta}\]

where \(u\) is a random number with uniform distribution in (0,1). The \(A\) and \(c\) parameters were computed in a logarithmic grid, ranging from 1 keV to 1.5 MeV with 100 points per decade. Since the \(g_2(\theta)\) function has a maximum at \(\theta = \frac{1}{\sqrt{c}}\), the \(c\) parameter was computed using the relation \(c=\frac{1}{\theta_{max}}\). At the point (\(k_{min},\theta_{max}\)) where \(k_{min}\) is the \(k\) cut value, the double differential cross-section has its maximum value, since it is monotonically decreasing in \(k\) and thus the global normalization parameter \(A\) is estimated from the relation:

\[A g_1(k_{min})g_2({\theta_{max}})= \left(\frac{d^2\sigma}{dkd\theta}\right)_{max}\]

where \(g_1(k_{min})g_2({\theta_{max}}) = \frac{k_{min}^{-b}}{2\sqrt{c}}\). Since \(A\) and \(c\) can only be retrieved for a fixed number of electron kinetic energies there exists the possibility that \(A g_1(k_{min})g_2({\theta_{max}})\le\left(\frac{d^2\sigma}{dkd\theta}\right)_{max}\) for a given \(E_k\). This is a small violation that can be corrected introducing an additional multiplicative factor to the \(A\) parameter, which was empirically determined to be 1.04 for the entire energy range.

Comparisons between Tsai, 2BS and 2BN generators

The currently available generators can be used according to the user required precision and timing requirements. Regarding the energy range, validation results indicate that for lower energies (\(\le\) 100 keV) there is a significant deviation on the most probable emission angle between Tsai/2BS generators and the 2BN generator - Fig. 27 to Fig. 29. The 2BN generator maintains however a good agreement with Kissel data [LKP83], derived from the work of Tseng and co-workers [HKTL79], and it should be used for energies between 1 keV and 100 keV [ea03]. As the electron kinetic energy increases, the different distributions tend to overlap and all generators present a good agreement with Kissel data.

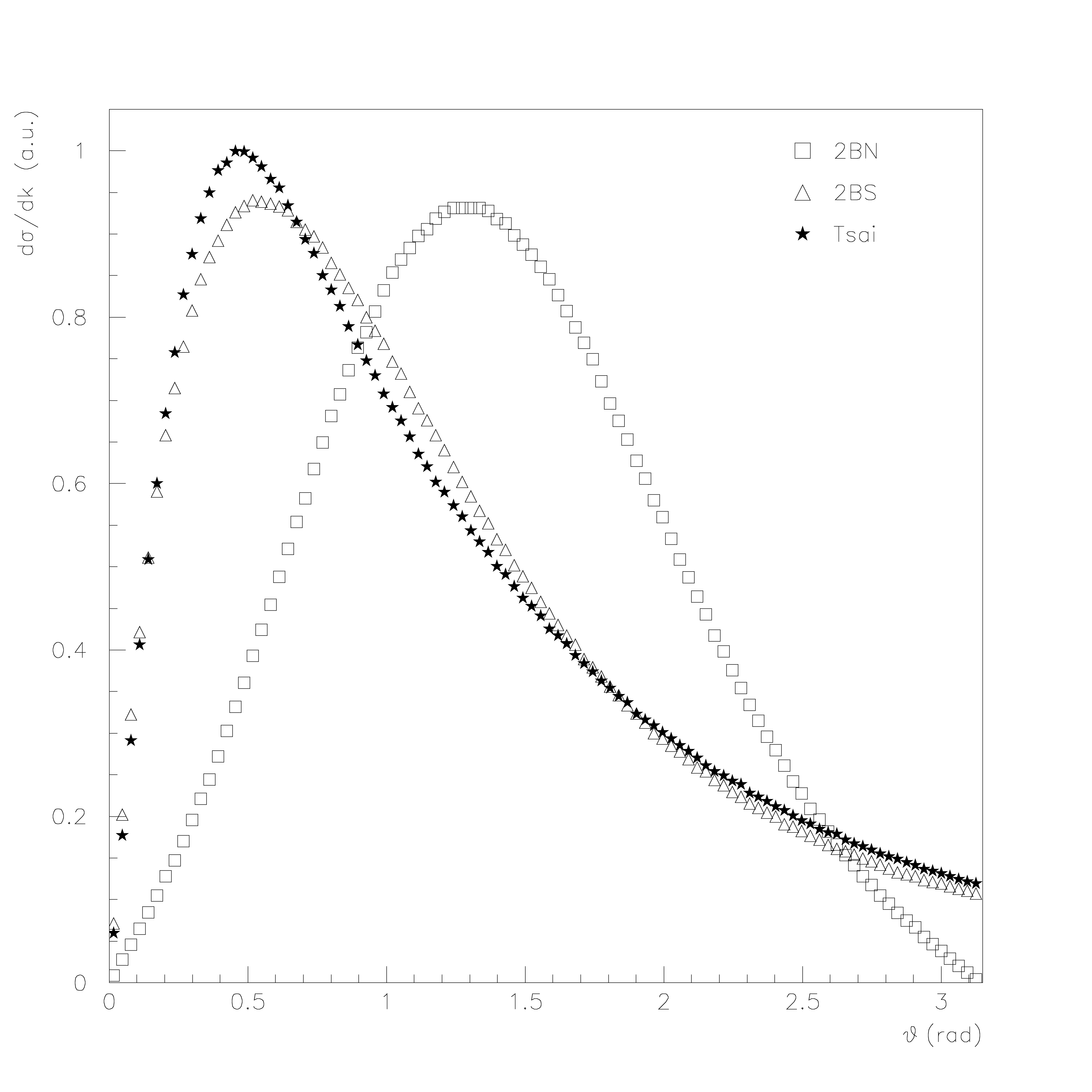
Fig. 27 Comparison of polar angle distribution of bremsstrahlung photons (\(k/T=0.5\)) for 10 keV electrons in silver, obtained with Tsai, 2BS and 2BN generator

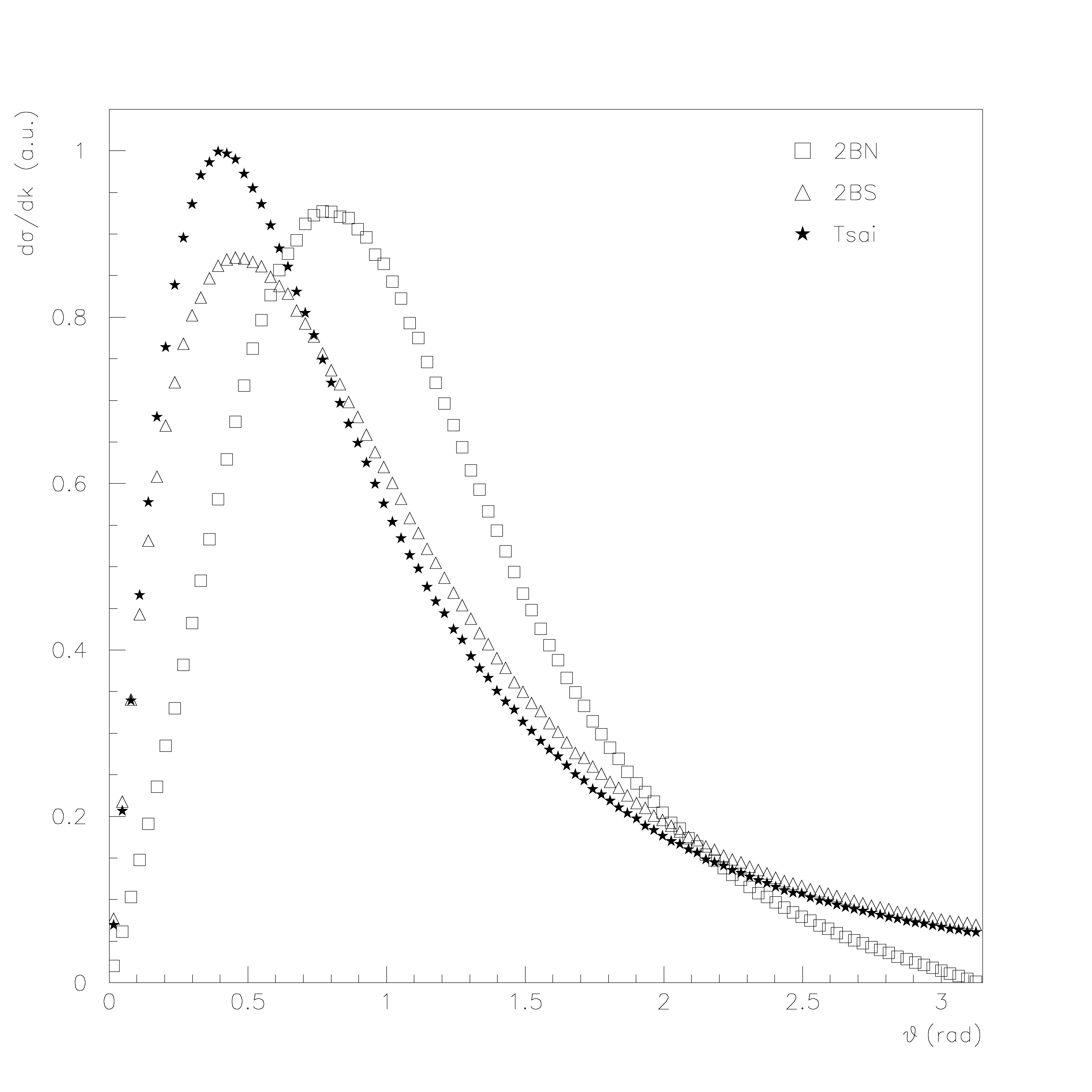
Fig. 28 Comparison of polar angle distribution of bremsstrahlung photons (\(k/T=0.5\)) for 100 keV electrons in silver, obtained with Tsai, 2BS and 2BN generator

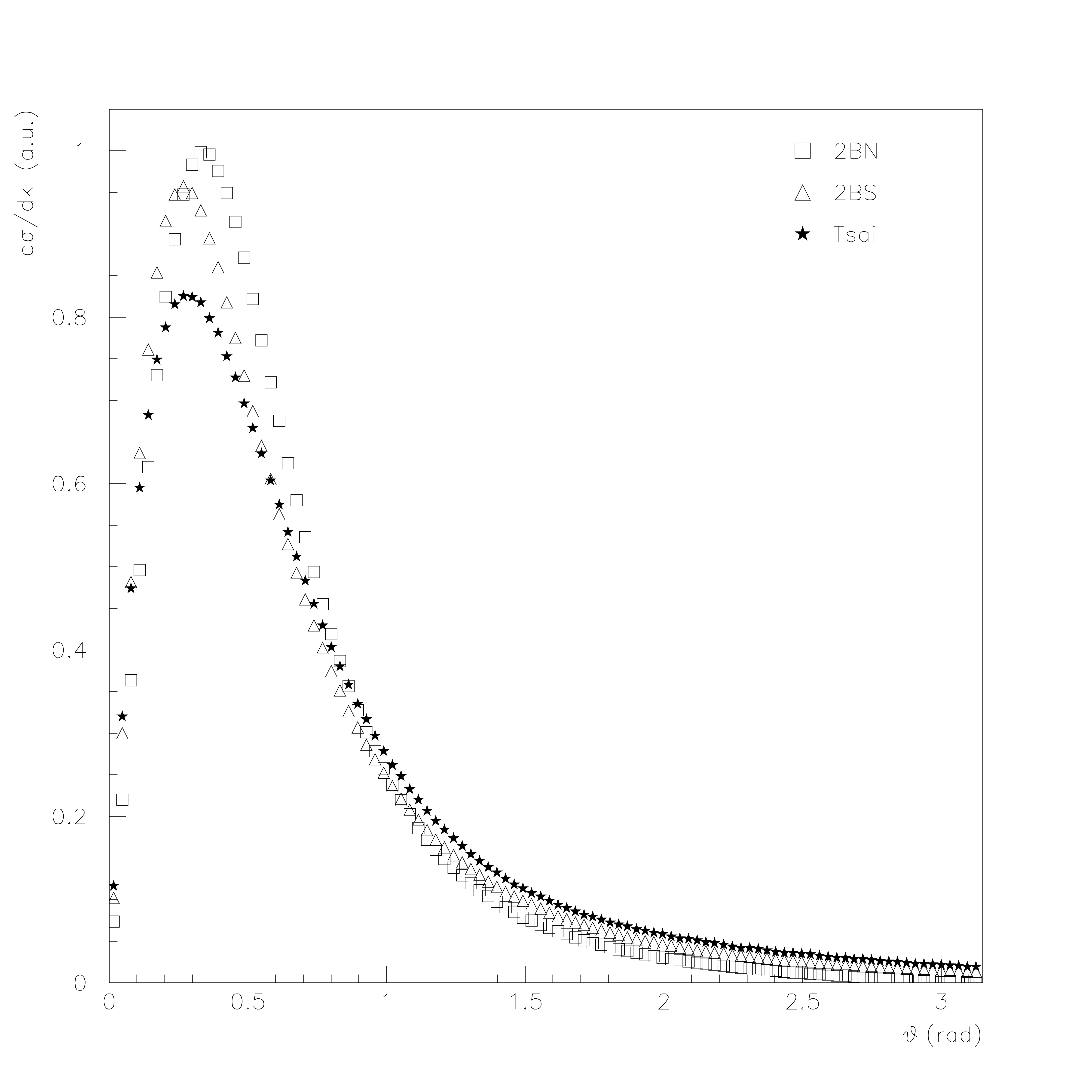
Fig. 29 Comparison of polar angle distribution of bremsstrahlung photons (\(k/T=0.5\)) for 500 keV electrons in silver, obtained with Tsai, 2BS and 2BN generator

In Fig. 30 the sampling efficiency for the different generators are presented. The sampling generation efficiency was defined as the ratio between the number of generated events and the total number of trials. As energies increases the sampling efficiency of the 2BN algorithm decreases from 0.65 at 1 keV electron kinetic energy down to almost 0.35 at 1 MeV. For energies up to 10 keV the 2BN sampling efficiency is superior or equivalent to the one of the 2BS generator. These results are an indication that precision simulation of low energy bremsstrahlung can be obtained with little performance degradation. For energies above 500 keV, Tsai generator can be used, retaining a good physics accuracy and a sampling efficiency superior to the 2BS generator.

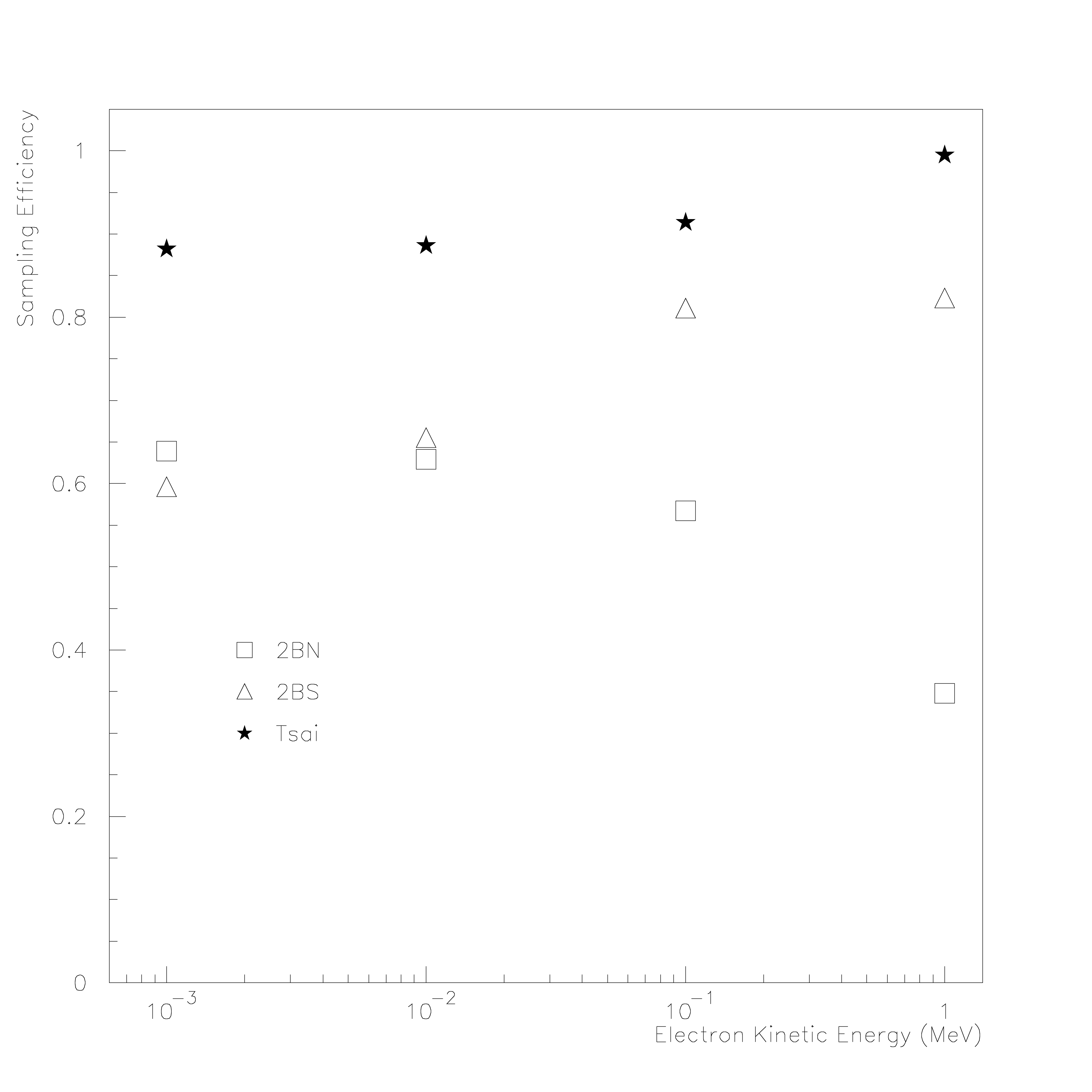
Fig. 30 Sampling efficiency for Tsai generator, 2BS and 2BN Koch and Motz generators.

Bibliography

AFBC89

R. Mohan A. F. Bielajew and C.-S. Chui. Improved bremsstrahlung photon angular sampling in the egs4 code system. Technical Report, 1989. Report NRCC/PIRS-0203.

ea03

P. Rodrigues et al. Geant4 applications and developments for medical physics experiments. IEEE NSS/MIC Conference Record, ():, 2003.

eal99

J. Apostolakis et al. Geant4 low energy electromagnetic models for electrons and photons. Technical Report, CERN, CERN/INFN, 1999. CERN-OPEN-99-034(1999), INFN/AE-99/18.

eal93

René Brun et al. GEANT: Detector Description and Simulation Tool; Oct 1994. CERN Program Library. CERN, Geneva, 1993. Long Writeup W5013. URL: https://cds.cern.ch/record/1082634.

HKTL79

R. H. Pratt H. K. Tseng and C. M. Lee. Electron bremsstrahlung angular distributions in the 1-500 kev energy range. Phys. Rev. A, 19():187, 1979.

KM59(1,2)

H. W. Koch and J. W. Motz. Bremsstrahlung cross-section formulas and related data. Rev. Mod. Phys., 31(4):920–955, 1959.

LKP83

C. A. Quarls L. Kissel and R. H. Pratt. Bremsstrahlung from electron collisions with neutral atoms. Atom. Data Nucl. Data Tables, 28():382, 1983.

STPerkins89(1,2)

S.M.Seltzer S.T.Perkins, D.E.Cullen. Tables and graphs of electron-interaction cross-sections from 10 ev to 100 gev derived from the llnl evaluated electron data library (eedl), z=1-100. Technical Report UCRL-50400 Vol.31, Lawrence Livermore National Laboratory, 1989.

Tsa74

Y. Tsai. Pair production and bremsstrahlung of charged leptons. Rev. Mod. Phys., 46():815, 1974.

Tsa77

Y. Tsai. Pair production and bremsstrahlung of charged leptons. Rev. Mod. Phys., 49():421, 1977.