Decays of orthopositronium at rest to 3 photons
Triplet state positronium, “orthopositronium”, is a spin-one state that decays to three photons. For a decay at rest, the three photons are emitted in a plane. The orientation of that plane and the polarization of the photons in the final state depend on the polarization of the positronium in the initial state.
For positronium decay at rest two ortho-positronium decay into 3 gamma
models are available: G4OrePowellAtRestModel with random polarization
and G4PolarizedOrePowellAtRestModel for arbitrary positronium and photon
polarization.
Random polarization
The decay for a positronium random polarization and summing on the
polarization of the photons is provided by G4OrePowellAtRestModel.
The differential decay rate is [OP49]:
where \(k_i\) and \(\Omega_i\) are the energy and solid angle of photon \(i\) and \(\theta_{ij}\) is the angle between the photon momenta \(\vec k_i\) and \(\vec k_j\). \(k_3\) and the directions of photons 2 and 3 are obtained from energy-momentum conservation. The photon energies sum up to \(k_1 + k_2 + k_3 = 2 m\), given the positronium mass is approximately equal to twice the electron mass, \(m\). Upon integration, one obtains the inclusive photon energy spectrum [OP49]:
with \(x \equiv k / m\), and \(0 \le x \le 1\), that is,
The graph of \(F(x)\) is given in Fig. 1.
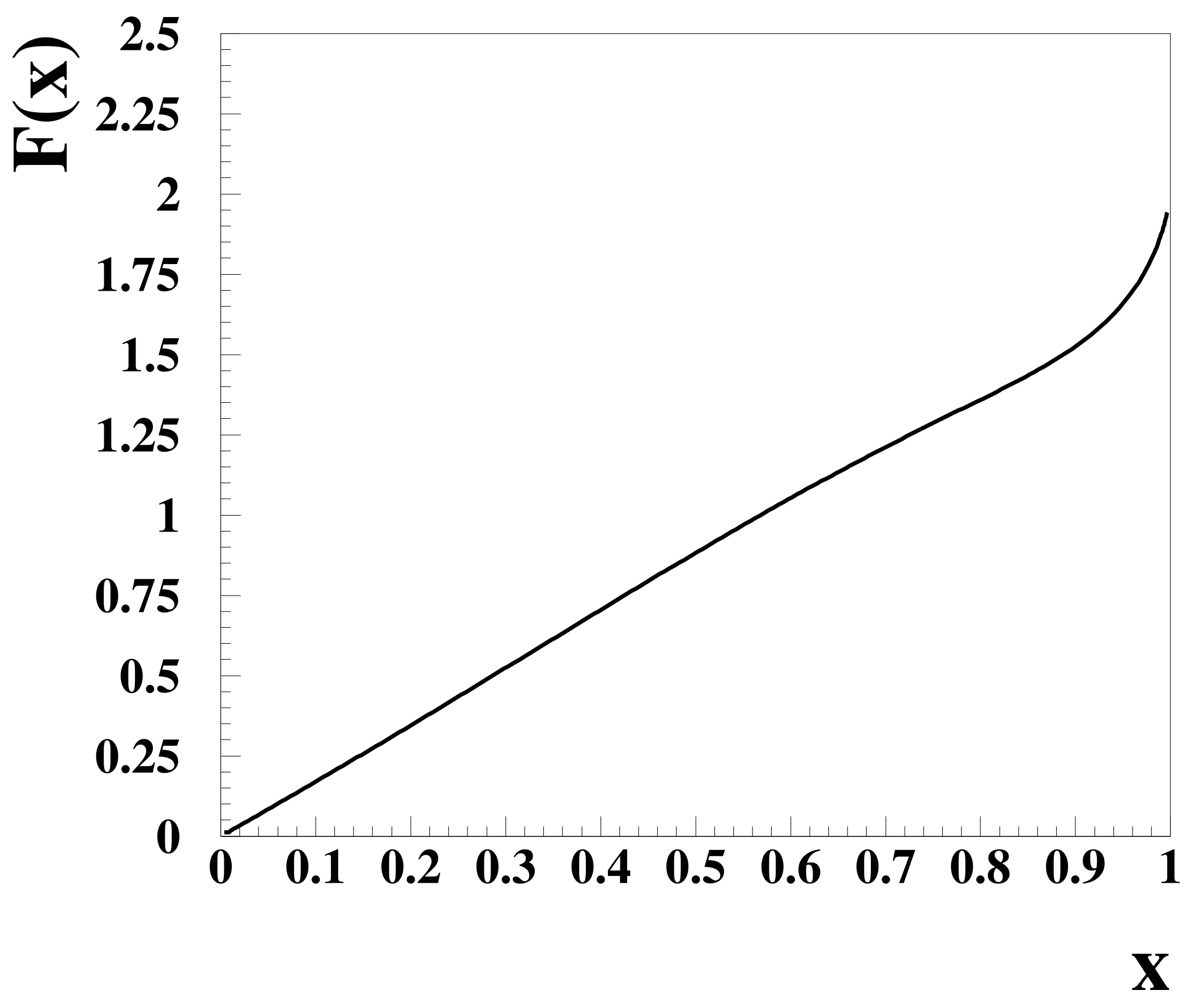
Fig. 1 Graph of \(F(x)\) ((2)).
The model samples the final state as follows
take \(k_1\) and \(k_2\) at random in \([0,m]\); compute \(k_3 = 2m - (k_1 + k_2)\);
assume \(k_1\) along \(\vec x\); compute \(\cos{\theta_{1i}}\), \(i=2,3\) from momentum conservation; request \(| \cos{\theta_{1i}} | \le 1\), \(i=2,3\); compute \(\cos{\theta_{23} }\) from \(\vec k_2 \cdot \vec k_3\);
generate events from pdf (1).
The direction of \(\vec k_1\) in the plane and the direction of the normal to the plane in the local frame are then taken at random and the final state rotated to the local frame accordingly.
Polarized model
The decay for arbitrary positronium and photon polarizations is provided
by G4PolarizedOrePowellAtRestModel. The differential decay rate
becomes proportional to
\(\left| (\vec t_1 + \vec t_2 + \vec t_3) \cdot \vec u \right|^2\)
[Dri56, OP49],
\(\vec u\) is a complex unit vector which characterizes the initial triplet state of the positronium atom;
\(\vec t_1 = -\vec a_3(\vec a_1.\vec a_2) +\vec a_1(\vec a\,'_2.\vec a\,'_3) -\vec a\,'_2(\vec a\,'_3.\vec a_1) -\vec a\,'_3(\vec a_1.\vec a\,'_2)\) and \(\vec t_2\) and \(\vec t_3\) are obtained by permutation of the photon indices (terms that cancel upon the sum \((\vec t_1 + \vec t_2 + \vec t_3)\) have been removed).
\(\vec a_i\) is the polarization vector of photon \(i\) and \(\vec a\,'_i = \vec a_i \times \vec n_i\), \(\vec n_i = \vec k_i / k_i\).
\(\vec u\) depends on the value of the positronium polarization quantum number, \(m\). If the quantization axis is perpendicular to the decay plane [Dri56, OP49]:
\(m=0\), \(\vec u = (0,0,1)\),
\(m=+1\), \(\vec u = (1,i,0)/\sqrt{2}\),
\(m=-1\), \(\vec u = (1,-i,0)/\sqrt{2}\),
where \(i\) is the imaginary unit.
The model samples the final state as follows
The direction of the positronium quantization axis is assumed to be \(\vec z\) in the local frame. Fill \(\vec u\) depending on input value of \(m\).
Take the orientation of the decay frame with respect to the local frame at random.
Generate a decay in the decay plane.
For each photon \(i\), compute \(\vec n_i\); compute vector perpendicular to \(\vec n_i\) in the horizontal plane, \(\vec m_i\);
take polarization vector in (\(\vec m_i, \vec z\)) plane, \(\vec z\) perpendicular to the decay plane (take \(\phi_i\) at random flat, \(\vec a_i = \cos(\phi_i) \vec m_i + \sin(\phi_i) \vec z\)); compute \(\vec a\,'_i = \vec a_i \times \vec n_i\);
Compute \(\vec t = (\vec t_1 + \vec t_2 + \vec t_3)\); rotate \(\vec t\) to the local frame. Compute \(\left| \vec t \cdot \vec u \right|^2\);
Generate events from pdf proportional to \(\left| \vec t \cdot \vec u \right|^2\).
Validation.
The inclusive energy spectra are found to be compatible with (2) and Fig. 1.
The distribution of the angle \(\theta\) between the quantization axis and the normal to the plane is found to be compatible with \({1}/{\Gamma} {\mathrm{d}\Gamma}/{\mathrm{d}\Omega}\) [BN81] (\(\mathrm{d}\Omega =\sin\theta \, \mathrm{d}\theta\)), that is, proportional to \((1+ \cos^2\theta)\) for \(m=0\) and to \((3 - \cos^2\theta)\) for \(m=\pm 1\).
Also in a dedicated version of the model for which the normal to the plane was set parallel to the quantization axis, it was checked that in the symmetric equipartition case, (\(\theta_{12} = \theta_{23} = \theta_{13} = 120^\circ\), \(k_1 = k_2 = k_3 = 2 m / 3\)), “the ratio of the number of quanta polarized perpendicular to the plane of the quanta to the number polarized in the plane of detection of the quanta is 5:1 when the positronium atom annihilates from the triplet \(m= 0\) state, 2:1 for the \(m= \pm1\) states” [Dri56].
The polarized model G4PolarizedOrePowellAtRestModel is approximately
one order of magnitude slower than the random polarization model
G4OrePowellAtRestModel.
- BN81
W. Bernreuther and O. Nachtmann. Weak interaction effects in positronium. Zeitschrift für Physik C Particles and Fields, 11(3):235–245, September 1981. URL: http://dx.doi.org/10.1007/BF01545680, doi:10.1007/bf01545680.
- Dri56(1,2,3)
R. M. Drisko. Spin and polarization effects in the annihilation of triplet positronium. Physical Review, 102(6):1542–1544, June 1956. URL: http://dx.doi.org/10.1103/PhysRev.102.1542, doi:10.1103/physrev.102.1542.
- OP49(1,2,3,4)
A. Ore and J. L. Powell. Three-photon annihilation of an electron-positron pair. Physical Review, 75(11):1696–1699, June 1949. URL: http://dx.doi.org/10.1103/PhysRev.75.1696, doi:10.1103/physrev.75.1696.