Single Scattering

Single elastic scattering process is an alternative to the multiple scattering process. The advantage of the single scattering process is in possibility of usage of theory based cross sections, in contrary to the Geant4 multiple scattering model [Urb06], which uses a number of phenomenological approximations on top of Lewis theory. The process G4CoulombScattering was created for simulation of single scattering of muons, it also applicable with some physical limitations to electrons, muons and ions. Because each of elastic collisions are simulated the number of steps of charged particles significantly increasing in comparison with the multiple scattering approach, correspondingly its CPU performance is poor. However, in low-density media (vacuum, low-density gas) multiple scattering may provide wrong results and single scattering processes are more appropriate.

Coulomb Scattering

The single scattering model of Wentzel [Wen27] is used in many multiple scattering models including the Penelope code [JMFernandezVS93]. The Wentzel model for describing elastic scattering of particles with charge \(ze\) (\(z=-1\) for electron) by atomic nucleus with atomic number \(Z\) is based on simplified scattering potential

\[V(r) = \frac {zZe^2}{r}\exp(-r/R),\]

where the exponential factor tries to reproduce the effect of screening. The parameter \(R\) is a screening radius [Bet53]

\[R = 0.885 Z^{-1/3} r_B,\]

where \(r_B\) is the Bohr radius. In the first Born approximation the elastic scattering cross section \(\sigma^{(W)}\) can be obtained as

(61)\[\frac{d\sigma^{(W)}(\theta)}{d\Omega} = \frac{(ze^2)^2}{(p\beta c)^2}\frac{Z(Z+1)}{(2A + 1 - \cos\theta)^2},\]

where \(p\) is the momentum and \(\beta\) is the velocity of the projectile particle. The screening parameter \(A\) according to Moliere and Bethe [Bet53]

\[A = \left(\frac{\hslash}{2pR}\right)^2(1.13 + 3.76(\alpha Z/\beta)^2),\]

where \(\alpha\) is the fine structure constant and the factor in brackets is used to take into account second order corrections to the first Born approximation. The total elastic cross section \(\sigma\) can be expressed via Wentzel cross section (61):

(62)\[\frac{d\sigma(\theta)}{d\Omega}= \frac{d\sigma^{(W)}(\theta)}{d\Omega}\left(\frac{Z}{(1 + \frac{(qR_N)^2}{12})^2} + 1\right)\frac{1}{Z + 1},\]

where \(q\) is momentum transfer to the nucleus, \(R_N\) is nuclear radius. This term takes into account nuclear size effect [eal02], the second term takes into account scattering off electrons. The results of simulation with the single scattering model (Fig. 20) are competitive with the results of the multiple scattering.

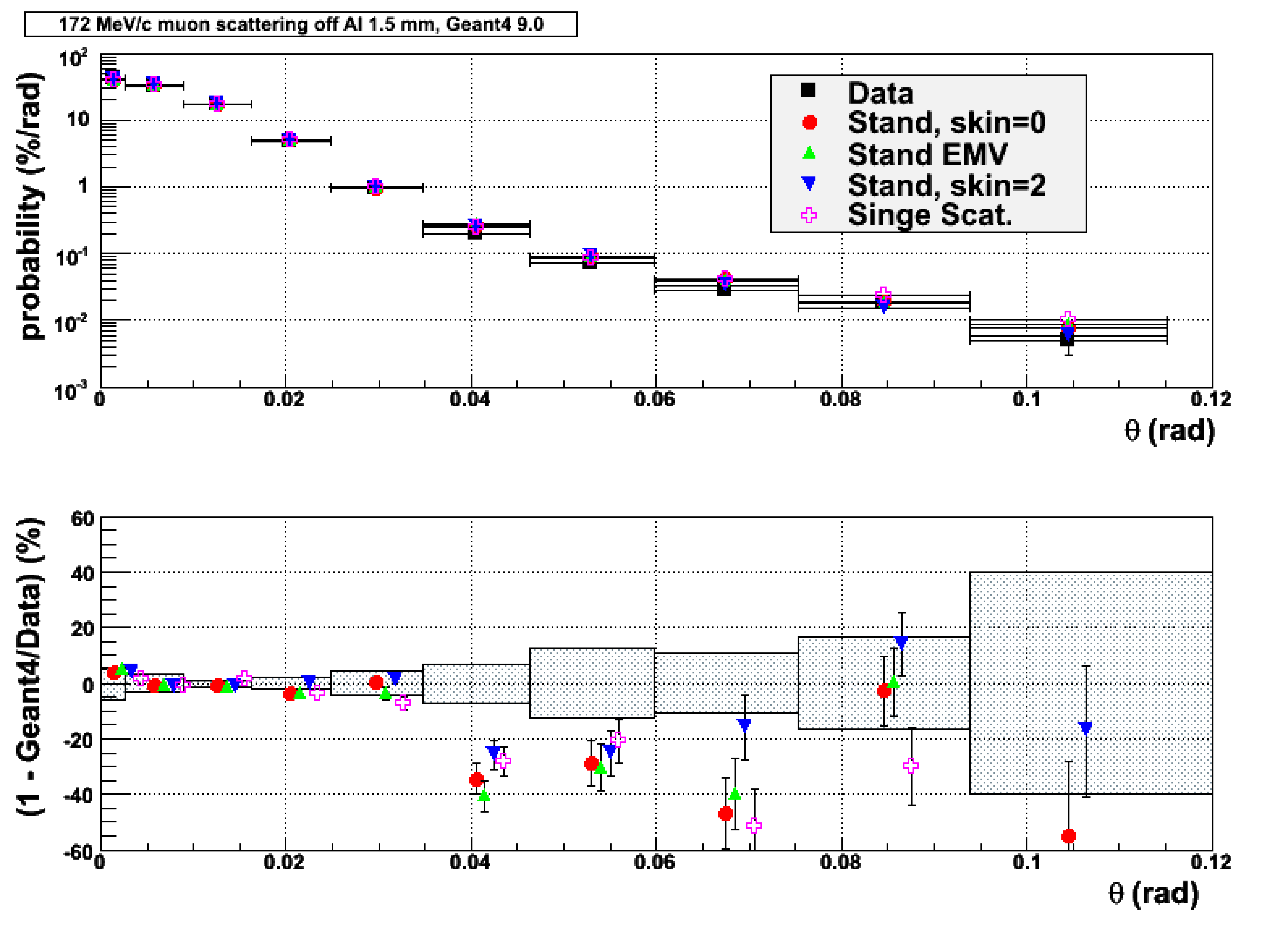
Fig. 20 Scattering of muons off 1.5 mm aluminum foil: data [eal06] - black squares; simulation - colored markers corresponding different options of multiple scattering and single scattering model; in the bottom plot - relative difference between the simulation and the data in percents; hashed area demonstrates one standard deviation of the data.

Implementation Details

The total cross section of the process is obtained as a result of integration of the differential cross section (62). The first term of this cross section is integrated in the interval \((0,\pi)\). The second term in the smaller interval \((0,\theta_m)\), where \(\theta_m\) is the maximum scattering angle off electrons, which is determined using the cut value for the delta electron production. Before sampling of angular distribution the random choice is performed between scattering off the nucleus and off electrons.

Bibliography

Bet53(1,2)

H.A. Bethe. Phys. Rev., 89:1256, 1953.

eal02

A.V. Butkevich et al. Nuclear Instruments and Methods in Physics Research A, 488:282, 2002.

eal06

D. Attwood et al. Nuclear Instruments and Methods in Physics Research B, 251:41, 2006.

JMFernandezVS93

J. Baró J.M. Fernández-Varea, R. Mayol and F. Salvat. On the theory and simulation of multiple elastic scattering of electrons. Nucl. Instrum. and Meth. in Phys. Research B, 73:447–473, apr 1993. doi:10.1016/0168-583X(93)95827-R.

Urb06

L. Urban. A multiple scattering model. Technical Report CERN-OPEN-2006-077, CERN, Dec 2006. 18 pp.

Wen27

G. Wentzel. Z. Phys., 40:590, 1927.