The class G4eBremsstrahlung provides the energy loss of electrons and positrons due to the radiation of photons in the field of a nucleus according to the approach described in Mean Energy Loss. Above a given threshold energy the energy loss is simulated by the explicit production of photons. Below the threshold the emission of soft photons is treated as a continuous energy loss.

Below electron/positron energies of 1 GeV, the cross section evaluation is based on a dedicated parameterization, above this limit an analytic cross section is used. In Geant4 the Landau-Pomeranchuk-Migdal effect has also been implemented.

Seltzer-Berger bremsstrahlung model

In order to improve accuracy of the model described above a new model G4SeltzerBergerModel have been design which implementing cross section based on interpolation of published tables [SB85, SB86]. Single-differential cross section can be written as a sum of a contribution of bremsstrahlung produced in the field of the screened atomic nucleus \(d\sigma_{n}/dk\), and the part \(Z\,d\sigma_{e}/dk\) corresponding to bremsstrahlung produced in the field of the Z atomic electrons,

\[\frac{d\sigma}{dk}=\frac{d\sigma_{n}}{dk}+Z\frac{d\sigma_{e}}{dk} \,.\]

The differential cross section depends on the energy \(k\) of the emitted photon, the kinetic energy \(T_{1}\) of the incident electron and the atomic number \(Z\) of the target atom.

Seltzer and Berger have published extensive tables for the differential cross section \(d\sigma_{n}/dk\) and \(d\sigma_{e}/dk\) [SB85, SB86], covering electron energies from 1 keV up to 10 GeV, substantially extending previous publications [eal77]. The results are in good agreement with experimental data, and provided also the basis of bremsstrahlung implementations in many Monte Carlo programs (e.g. Penelope, EGS). The estimated uncertainties for \(d\sigma/dk\) are:

3% to 5% in the high energy region (\(T_{1}\geq 50\) MeV),
5% to 10% in the intermediate energy region (\(2 \geq T_{1}\leq 50\) MeV),
and 10% at low energies region compared with Pratt results. (\(T_{1}\leq 2\) MeV).

The restricted cross section (32) and the energy loss (33) are obtained by numerical integration performed at initialisation stage of Geant4. This method guarantees consistent description independent of the energy cutoff. The current version uses an interpolation in tables for 52 available electron energy points versus 31 photon energy points, and for atomic number Z ranging from 1 to 99. It is the default bremsstrahlung model in Geant4 since version 9.5. Fig. 27 shows a comparison of the total bremsstrahlung cross sections with the previous implementation, and with the relativistic model.

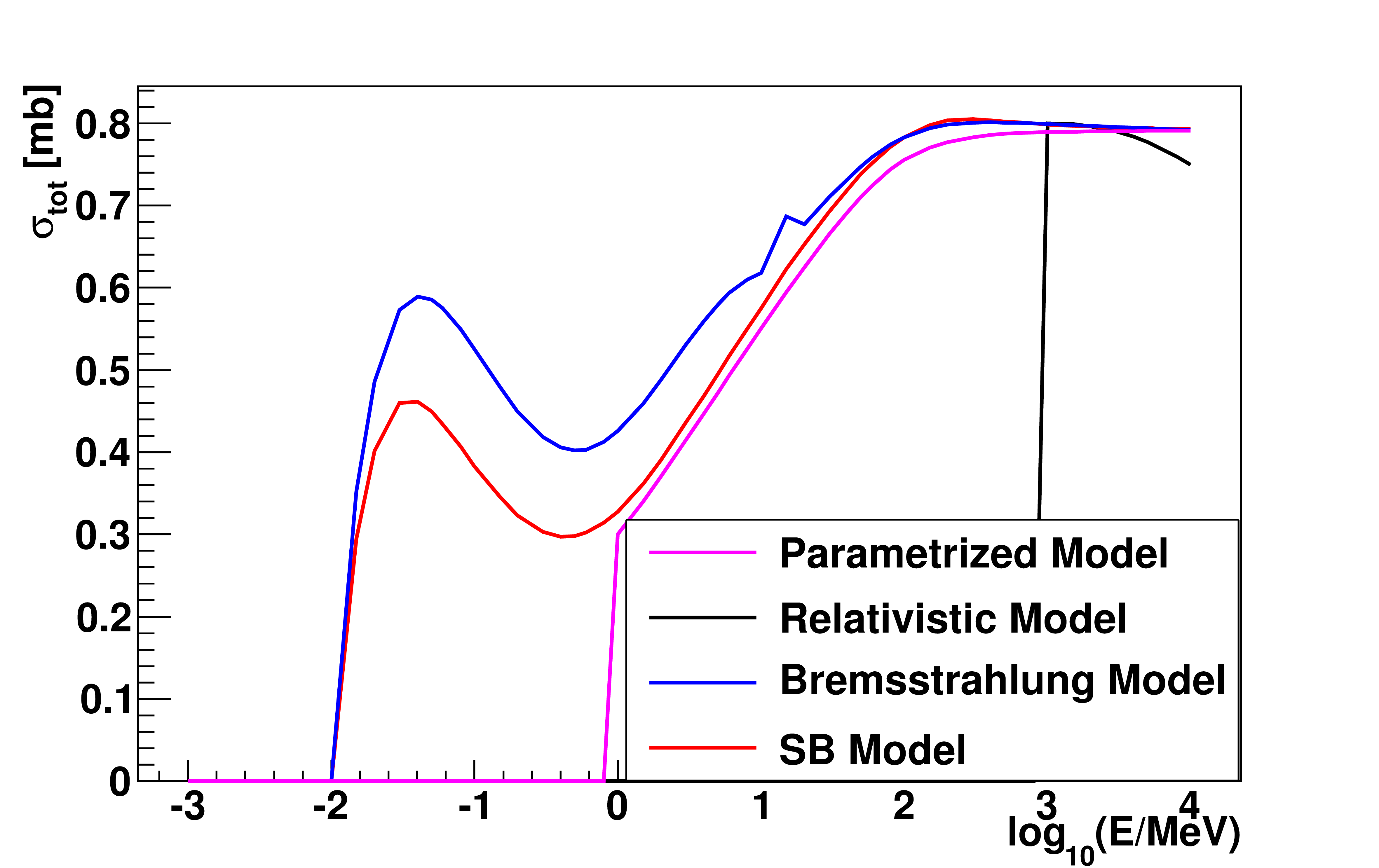
Fig. 27 Total cross section comparison between models for \(Z = 29\): Parametrized Bremsstrahlung Model, Relativistic Model, Bremsstrahlung Model (Geant4 9.4) and Seltzer-Berger Model. The discontinuities in the Paramretized Model and the Relativistic Model at 1 Mev and 1 GeV, respectively, mark the validity range of these models.

After the successful sampling of \(\epsilon\), the polar angles of the radiated photon are generated with respect to the parent electron’s momentum. It is difficult to find simple formulae for this angle in the literature. For example the double differential cross section reported by Tsai [Tsa74, Tsa77] is

\[\begin{split}\frac{d \sigma}{dkd \Omega} & = \frac{2 \alpha^{2}e^{2}}{\pi k m^{4}} \left\{ \left[ \frac{2\epsilon-2}{(1+u^2)^2}+ \frac{12u^2(1-\epsilon)}{(1+u^2)^4}\right] Z(Z+1) \right. \\ &+ \left. \left[ \frac{2-2\epsilon-\epsilon^{2}}{(1+u^2)^2}- \frac{4u^2(1-\epsilon)}{(1+u^2)^4} \right] \left[ X-2Z^{2}f_{c}((\alpha Z)^{2})\right] \right\} \\ u & = \frac{E \theta}{m} \\ X & = \int_{t_{min}}^{m^{2}(1+u^{2})^{2}} {\left [ G_{Z}^{el}(t) + G_{Z}^{in}(t) \right ] \frac{t-t_{min}} {t^{2}} dt} \\ G_{Z}^{el, in}(t) &: \mbox{atomic form factors} \\ t_{min} & = \left [ \frac{k m^{2} (1+u^{2})}{2 E (E-k)} \right ] ^{2} = \left [ \frac{\epsilon m^{2} (1+u^{2})}{2 E (1-\epsilon)} \right ] ^{2} .\end{split}\]

The sampling of this distribution is complicated. It is also only an approximation to within a few percent, due at least to the presence of the atomic form factors. The angular dependence is contained in the variable \(u = E \theta m^{-1}\). For a given value of \(u\) the dependence of the shape of the function on \(Z\), \(E\) and \(\epsilon = k/E\) is very weak. Thus, the distribution can be approximated by a function

\[f(u) = C \left( u e^{-au} + d u e^{-3au} \right)\]

where

\[C = \frac{9a^{2}}{9 + d} \hspace{1cm} a = 0.625 \hspace{1cm} d = 27\]

where \(E\) is in GeV. While this approximation is good at high energies, it becomes less accurate around a few MeV. However in that region the ionisation losses dominate over the radiative losses. The sampling of the function \(f(u)\) can be done with three random numbers \(r_i\), uniformly distributed on the interval [0,1]:

choose between \(u e^{-au}\) and \(d u e^{-3au}\):

\[\begin{split}b = \left \{ \begin{array}{lll} a & \mbox{if} & r_{1} < 9/(9+d) \\ 3a & \mbox{if} & r_{1} \geq 9/(9+d) \end{array} \right .\end{split}\]
sample \(u e^{-bu}\):

\[u=-\frac{\log ( r_{2} r_{3}) }{b}\]
check that:

\[u \leq u_{max} = \frac{E \pi}{m}\]

otherwise go back to 1.

The probability of failing the last test is reported in Table 19.

Table 19 Probability of failing test.
E (MeV)	P(%)
0.511	3.4
0.6	2.2
0.8	1.2
1.0	0.7
2.0	< 0.1

The function \(f(u)\) can also be used to describe the angular distribution of the photon in \(\mu\) bremsstrahlung and to describe the angular distribution in photon pair production. The azimuthal angle \(\phi\) is generated isotropically. Along with \(\theta\), this information is used to calculate the momentum vectors of the radiated photon and parent recoiled electron, and to transform them to the global coordinate system. The momentum transfer to the atomic nucleus is neglected.

Bremsstrahlung of high-energy electrons

Above an electron energy of 1 GeV an analytic differential cross section representation is used [Per94], which was modified to account for the density effect and the Landau-Pomeranchuk-Migdal (LPM) effect [eal82, Kle99].

Relativistic Bremsstrahlung cross section

The basis of the implementation is the well known high energy limit of the Bremsstrahlung process [Per94],

(140)\[\frac{d\sigma}{dk} = \frac{4 \alpha r_e^2}{3k} \biggl[ \{ y^2 + 2 [ 1 + (1-y)^2 ] \} [ Z^2 ( F_{el} - f ) + Z F_{inel} ] + (1-y) \frac{Z^2 + Z }{3} \biggr]\]

The elastic from factor \(F_{el}\) and inelastic form factor \(F_{inel}\), describe the scattering on the nucleus and on the shell electrons, respectively, and for \(Z>4\) are given by [eal08]

\[\begin{split}F_{el} & = \log\biggl( \frac{184.15}{Z^{\frac{1}{3}} } \biggr) \\ F_{inel} & = \log\biggl( \frac{1194.}{Z^{\frac{2}{3}} } \biggr) \;.\end{split}\]

This corresponds to the complete screening approximation. The Coulomb correction is defined as [eal08]

\[f = \alpha^2 Z^2 \sum_{n=1}^\infty \frac{1}{n ( n^2 + \alpha^2Z^2 )}\]

This approach provides an analytic differential cross section for an efficient evaluation in a Monte Carlo computer code. Note that in this approximation the differential cross section \(d\sigma/dk\) is independent of the energy of the initial electron and is also valid for positrons.

The total integrated cross section \(\int d\sigma/dk \, dk\) is divergent, but the energy loss integral \(\int k d\sigma/dk \, dk\) is finite. This allows the usual separation into continuous energy loss, and discrete photon production according to Eqs. (33) and (32).

Landau Pomeranchuk Migdal (LPM) effect

At higher energies matter effects become more and more important. In Geant4 the two leading matter effects, the LPM effect and the dielectric suppression (or Ter-Mikaelian effect), are considered. The analytic cross section representation, (140), provides the basis for the incorporation of these matter effects.

The LPM effect (see for example [eal04, eal97, GG64]) is the suppression of photon production due to the multiple scattering of the electron. If an electron undergoes multiple scattering while traversing the so called “formation zone”, the bremsstrahlung amplitudes from before and after the scattering can interfere, reducing the probability of bremsstrahlung photon emission (a similar suppression occurs for pair production). The suppression becomes significant for photon energies below a certain value, given by

\[\frac{k}{E} < \frac{E}{E_{LPM}} ,\]

where

\[\begin{split}\begin{array}{ll} k & \mbox{photon energy} \\ E & \mbox{electron energy} \\ E_{LPM} & \mbox{characteristic energy for LPM effect (depend on the medium).} \end{array}\end{split}\]

The value of the LPM characteristic energy can be written as

(141)\[E_{LPM} = \frac{\alpha m^2 X_0}{4 h c} ,\]

where

\[\begin{split}\begin{array}{ll} \alpha & \mbox{fine structure constant} \\ m & \mbox{electron mass} \\ X_0 & \mbox{radiation length in the material} \\ h & \mbox{Planck constant} \\ c & \mbox{velocity of light in vacuum.} \end{array}\end{split}\]

At high energies (approximately above 1 GeV) the differential cross section including the Landau-Pomeranchuk-Migdal effect, can be expressed using an evaluation based on [eal82, Kle99, Mig56]

(142)\[\begin{split}\frac{d\sigma}{dk} = \frac{4 \alpha r_e^2}{3k} \biggl[ \xi(s) \{ y^2 G(s) + 2 [ 1 + (1-y)^2 ] \phi(s) \} \\ \times [ Z^2 (F_{el} - f ) + Z F_{inel} ] + (1-y) \frac{Z^2 + Z }{3} \biggr]\end{split}\]

where LPM suppression functions are defined by [Mig56]

\[G(s) = 24s^2 \biggl( \frac{\pi}{2} - \int_0^\infty e^{-st} \frac{\sin(st)}{\sinh(\frac{t}{2})} dt\biggr)\]

and

\[\phi(s) = 12s^2 \Biggl( -\frac{\pi}{2} + \int_0^\infty e^{-st} \sin(st) \sinh\Bigl(\frac{t}{2}\Bigr)\, dt\Biggr)\]

They can be piecewise approximated with simple analytic functions, see e.g. [eal82]. The suppression function \(\xi(s)\) is recursively defined via

\[s = \sqrt{ \frac{k\,E_{\rm LPM} }{8 E(E-k) \xi(s)} }\]

but can be well approximated using an algorithm introduced by [eal82]. The material dependent characteristic energy \(E_{\rm LPM}\) is defined in Eq.(141) according to [eal97]. Note that this definition differs from other definition (e.g. [Kle99]) by a factor \(\frac{1}{2}\).

An additional multiplicative factor governs the dielectric suppression effect (Ter-Mikaelian effect) [TER54].

\[S(k) = \frac{k^2}{k^2+k_p^2}\]

The characteristic photon energy scale \(k_p\) is given by the plasma frequency of the media, defined as

\[k_p = \hbar \omega_p \frac{E_e}{m_e c^2} = \frac{\hbar E_e}{m_e c^2}\cdot \sqrt{\frac{n_e e^2}{\epsilon_0 m_e} } \;.\]

Both suppression effects, dielectric suppression and LPM effect, reduce the effective formation length of the photon, so the suppressions do not simply multiply. A consistent treatment of the overlap region, where both suppression mechanism, was suggested by [TM72]. The algorithm guaranties that the LPM suppression is turned off as the density effect becomes important. This is achieved by defining a modified suppression variable \(\hat{s}\) via

\[\hat{s} = s \cdot \biggl( 1 + \frac{k_p^2}{k^2} \biggr)\]

and using \(\hat{s}\) in the LPM suppression functions \(G(s)\) and \(\phi(s)\) instead of \(s\) in Eq.(142).

Bibliography

eal08(1,2): C. Amsler et al. Review of particle physics. Physics Letters B, 667(1-5):1–6, sep 2008. URL: https://doi.org/10.1016/j.physletb.2008.07.018, doi:10.1016/j.physletb.2008.07.018.
eal04: H.D. Hansen et al. Landau-pomeranchuk-migdal effect for multihundred gev electrons. Physical Review D, feb 2004. URL: https://doi.org/10.1103/PhysRevD.69.032001, doi:10.1103/physrevd.69.032001.
eal97(1,2): P. L. Anthony et al. Bremsstrahlung suppression due to the landau-pomeranchuk-migdal and dielectric effects in a variety of materials. Physical Review D, 56(3):1373–1390, aug 1997. URL: https://doi.org/10.1103/PhysRevD.56.1373, doi:10.1103/physrevd.56.1373.
eal77: R.H. Pratt et al. Bremsstrahlung energy spectra from electrons of kinetic energy 1 keV ≤ t1 ≤ 2000 keV incident on neutral atoms 2 ≤ z ≤ 92. Atomic Data and Nuclear Data Tables, 20(2):175–209, aug 1977. URL: https://doi.org/10.1016/0092-640X(77)90045-6, doi:10.1016/0092-640x(77)90045-6.
eal82(1,2,3,4): T. Stanev et al. Development of ultrahigh-energy electromagnetic cascades in water and lead including the landau-pomeranchuk-migdal effect. Physical Review D, 25(5):1291–1304, mar 1982. URL: https://doi.org/10.1103/PhysRevD.25.1291, doi:10.1103/physrevd.25.1291.
GG64: V.M. Galitsky and I.I. Gurevich. Coherence effects in ultra-relativistic electron bremsstrahlung. Il Nuovo Cimento (1955-1965), 32(2):396–407, Apr 1964. URL: https://doi.org/10.1007/BF02733969, doi:10.1007/BF02733969.
Kle99(1,2,3): Spencer Klein. Suppression of bremsstrahlung and pair production due to environmental factors. Reviews of Modern Physics, 71(5):1501–1538, oct 1999. URL: https://doi.org/10.1103/RevModPhys.71.1501, doi:10.1103/revmodphys.71.1501.
Mig56(1,2): A.B. Migdal. Bremsstrahlung and pair production in condensed media at high energies. Physical Review, 103(6):1811–1820, sep 1956. URL: https://doi.org/10.1103/PhysRev.103.1811, doi:10.1103/physrev.103.1811.
Per94(1,2): M.L. Perl. Notes on the Landau, Pomeranchuk, Migdal effect: Experiment and theory. In 8th Les Rencontres de Physique de la Vallee d'Aoste: Results and Perspectives in Particle Physics La Thuile, Italy, March 6-12, 1994. 1994. URL: http://www-public.slac.stanford.edu/sciDoc/docMeta.aspx?slacPubNumber=SLAC-PUB-6514.
SB85(1,2): S.M. Seltzer and M.J. Berger. Bremsstrahlung spectra from electron interactions with screened atomic nuclei and orbital electrons. Nucl. Instr. and Meth. in Phys. Research B, 12(1):95–134, aug 1985. URL: https://doi.org/10.1016/0168-583X(85)90707-4, doi:10.1016/0168-583x(85)90707-4.
SB86(1,2): S.M. Seltzer and M.J. Berger. Bremsstrahlung energy spectra from electrons with kinetic energy 1 kev - 100 gev incident on screened nuclei and orbital electrons of neutral atoms with z = 1–100. Atomic Data and Nuclear Data Tables, 35():345, 1986.
TM72: M.L. Ter-Mikaelian. High-energy Electromagnetic Processes in Condensed Media. Wiley, 1972.
TER54: ML TERMIKAELYAN. Spektr tormoznogo izlucheniya v srede. DOKLADY AKADEMII NAUK SSSR, 94(6):1033–1036, 1954.
Tsa74: Y. Tsai. Pair production and bremsstrahlung of charged leptons. Rev. Mod. Phys., 46():815, 1974.
Tsa77: Y. Tsai. Pair production and bremsstrahlung of charged leptons. Rev. Mod. Phys., 49():421, 1977.