X-ray reflection

X-rays impacting at small angles on surfaces can undergo specular reflection. This is simulated by the class G4XrayReflection implemented as a standard electromagnetic X-ray process for the gamma particle. Design criteria were, clarity, speed and modularity.

The implementation has a default reflection model and data for all stable elements and a simple surface roughness model. For specific cases like multilayer surfaces, it should be straightforward to replace the default reflection and roughness model by user provided models. The reflection model implemented is the one used by the Center for X-Ray Optics at Lawrence Berkeley National Laboratory CXRO for single layers, described and illustrated in the X-Ray Data Booklet as well as in X-Ray Interactions With Matter based on the paper from Henke et al. [HGD93] and their element data available in G4EMLOW since version 8.5 as formatted tables with 3 columns E(eV), f1, f2. The minimum energy is 10 eV and the maximum energy 30 keV spaced by 0.1 eV close to absorption edges. The number of points varies depending on the element between 505 and 909 points. The data below 30 eV has f1=-9999 and is not used in G4XrayReflection.

The wavelength \(\lambda\) of a photon is inversely proportional to its energy E, according to

\[\lambda = \frac{hc}{E}\]

where h is the Planck constant and c the speed of light. Numerically \(hc = 1.239\,842\,{\rm keV \; nm}\). The data can be used to calculate the complex reflection index

\[n = 1 - \delta - i \beta\]

as a function of energy, where \(\delta\) and \(\beta\) are obtained from \(f_1, f_2\) by multiplication with the number of atoms per unit volume N, the classical electron radius \(r_e\) and the wavelength squared, according to

\[\begin{split}\begin{aligned} \delta &=& \frac{N \, r_e \, \lambda^2}{2\pi} \; f_1 \nonumber \\ \beta &=& \frac{N \, r_e \, \lambda^2}{2\pi} \; f_2 \end{aligned}\end{split}\]

The values of \(\delta\), \(\beta\) are calculated and saved in the material tables by G4XrayReflection::SaveHenkeDataAsMaterialProperty from the values of \(f_1, f_2\) read from the data files by G4XrayReflection::ReadHenkeXrayData for all elements used in a particular simulation. This is done when the G4XrayReflection class is first created. For more details see [Bur25]. An example of how to use this process is provided with the extended electromagnetic example TestEm16.

Activation

The modeling is launched from G4XrayReflection::GetMeanFreePath for gamma energies between 30 eV and 30 keV when the gamma particle reaches a new volume. At this point the previous and new volume media, the gamma energy and direction and the surface normal are known and can be used to calculate the reflection probability. Reflection is only considered when the new medium has a higher density than the previous volume.

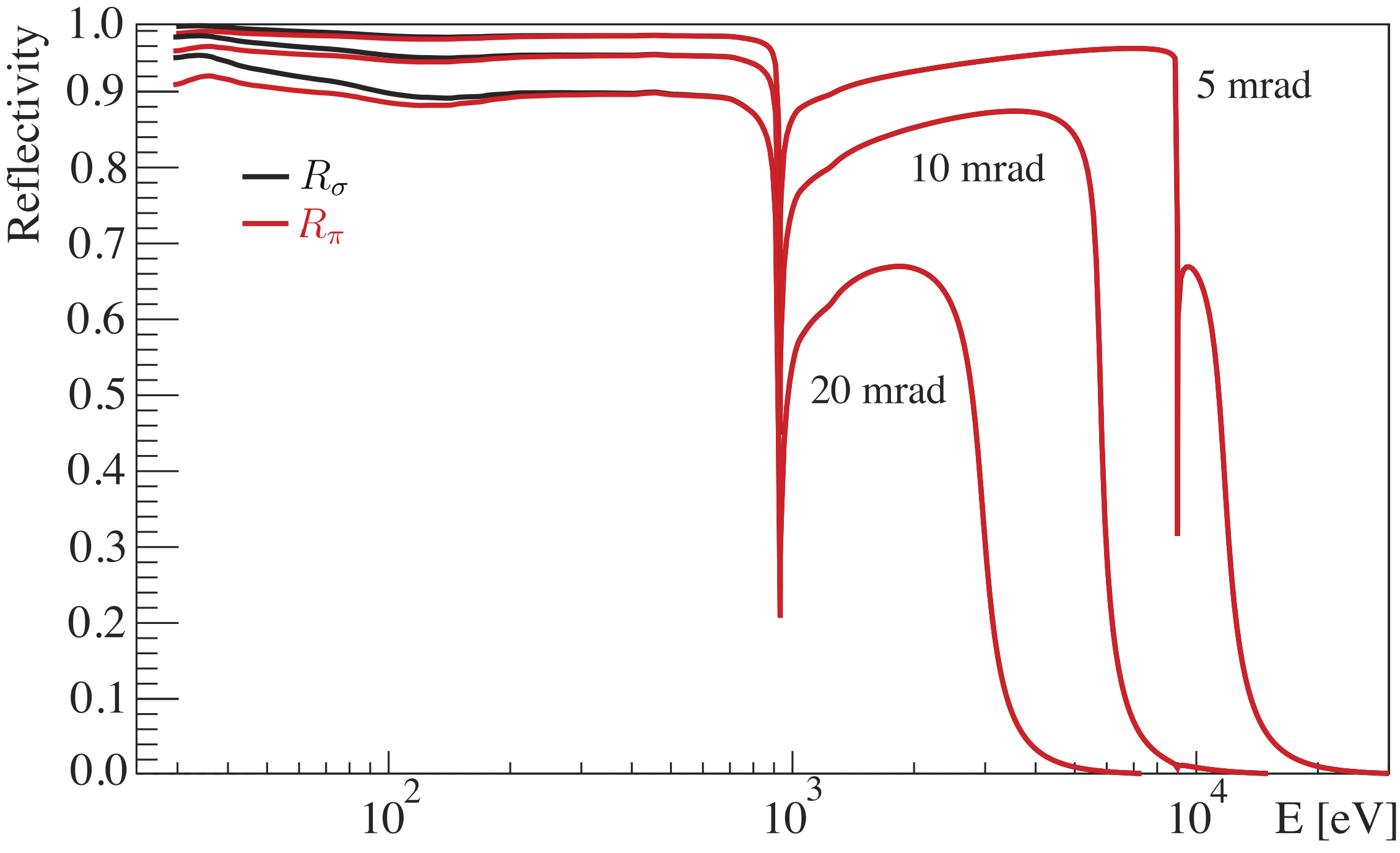
Reflectivity model

The reflectivity model implemented is that described by Henke et al. in section C. as “Non-Bragg Fresnel Reflection at Small Angles for the Semi-Infinite; Solid 1. Reflection from an Ideally Smooth Surface”. The reflection probability for the impact angle \(\theta\) is calculated as the average value of the \(\sigma\) and \(\pi\) polarization reflectivities

\[R_\sigma = \frac{ \rho^2(\sin\theta-\rho)^2 + \beta^2}{ \rho^2(\sin\theta+\rho)^2 + \beta^2}\]

and

\[R_\pi = R_\sigma \, \frac{ \rho^2(\rho-\cos\theta\cot\theta)^2 + \beta^2}{ \rho^2(\rho+\cos\theta\cot\theta)^2 + \beta^2}\]

where

\[\rho^2 = \frac{1}{2} \left[ \sin^2\theta - 2\delta + \sqrt{ (\sin^2\theta - 2\delta)^2 + 4\beta^2} \right]\,.\]

using the \(\delta, \beta\) values at the current gamma energy. Fig. 18 shows the reflectivity for copper calculated as described here and used by default in G4XrayReflection as a function of energy for three different impact angles.

../../../_images/henke_physical_reference_Cu_reflectivity_from_30eV.png

Fig. 18 Reflectivity of copper as a function of the photon energy for different impact angles \(\theta\).

Surface roughness model

Implemented is a simple exponential Névot–Croce [NC80] attenuation factor f:

\[\begin{split}\begin{aligned} k_{iz} &=& \frac{\sin\theta \, E_\gamma}{\hbar c}\\ \nonumber k_{jz} &=& (1-\delta) \, \frac{\sin\theta \, E_\gamma}{\hbar c}\\ \nonumber f &=& \exp( -2 \,k_{i,z} \, k_{j,z} \, \sigma^2 ) \end{aligned}\end{split}\]

where \(\sigma\) is the surface roughness. A typical value for a metallic surface can be 5 nm.

Bibliography

Bur25: H. Burkhardt. Technical Report, CERN, Geneva, 2025. To be published. URL: arXiv_nnnn.nnnnn.
HGD93: B.L. Henke, E.M. Gullikson, and J.C. Davis. X-ray interactions: photoabsorption, scattering, transmission, and reflection at e = 50-30,000 ev, z = 1-92. Atomic Data and Nuclear Data Tables, 54(2):181–342, July 1993. URL: http://dx.doi.org/10.1006/adnd.1993.1013, doi:10.1006/adnd.1993.1013.
NC80: L. Névot and P. Croce. Caractérisation des surfaces par réflexion rasante de rayons x. application à l’étude du polissage de quelques verres silicates. Revue de Physique Appliquée, 15(3):761–779, 1980. URL: http://dx.doi.org/10.1051/rphysap:01980001503076100, doi:10.1051/rphysap:01980001503076100.