Synchrotron Radiation
Photon spectrum
Synchrotron radiation photons are emitted by relativistic charged particles traveling in magnetic fields. The properties of synchrotron radiation are well understood and described in textbooks [Hof04, JDJackson98, ST86].
In the simplest case, we have an electron of momentum \(p\) moving perpendicular to a homogeneous magnetic field \(B\). The magnetic field will keep the particle on a circular path, with radius
In general, there will be an arbitrary angle \(\theta\) between the local magnetic field \({\bf B}\) and momentum vector \({\bf p}\) of the particle. The motion has a circular component in the plane perpendicular to the magnetic field, and in addition a constant momentum component parallel to the magnetic field. For a constant homogeneous field, the resulting trajectory is a helix.
The critical energy of the synchrotron radiation can be calculated using the radius \(\rho\) of Eq.(210) and angle \(\theta\) or the magnetic field perpendicular to the particle direction \(B_\perp = B \sin \theta\) according to
Half of the synchrotron radiation power is radiated by photons above the critical energy.
With \(x\) we denote the photon energy \(E_\gamma\), expressed in units of the critical energy \(E_c\)
The photon spectrum (number of photons emitted per path length \(s\) and relative energy \(x\)) can be written as
where \(\alpha = e^2 /\;4\pi\epsilon_0\hbar c\) is the dimensionless electromagnetic coupling (or fine structure) constant and \(K_{5/3}\) is the modified Bessel function of the third kind.
The number of photons emitted per unit length and the mean free path \(\lambda\) between two photon emissions is obtained by integration over all photon energies. Using
we find that
Here we are only interested in ultra-relativistic (\(\beta \approx 1\)) particles, for which \(\lambda\) only depends on the field \(B\) and not on the particle energy. We define a constant \(\lambda_B\) such that
As an example, consider a \(10\,{\rm GeV}\) electron, travelling perpendicular to a 1T field. It moves along a circular path of radius \(\rho = 33.356\,{\rm m}\). For the Lorentz factor we have \(\gamma = 19569.5\) and \(\beta= 1-1.4\times10^{-9}\). The critical energy is \(E_c = 66.5\,{\rm keV}\) and the mean free path between two photon emissions is \(\lambda = 0.16183\,{\rm m}\).
Validity
The spectrum given in Eq.(213) can generally be expected to provide a very accurate description for the synchrotron radiation spectrum generated by GeV electrons in magnetic fields.
Here we discuss some known limitations and possible extensions.
For particles traveling on a circular path, the spectrum observed in one location will in fact not be a continuous spectrum, but a discrete spectrum, consisting only of harmonics or modes \(n\) of the revolution frequency. In practice, the mode numbers will generally be too high to make this a visible effect. The critical mode number corresponding to the critical energy is \(n_c = 3/2\,\gamma^3\). 10GeV electrons for example have \(n_c \approx 10^{13}\).
Synchrotron radiation can be neglected for slower particles and only becomes relevant for ultra-relativistic particles with \(\gamma > 10^3\). Using \(\beta = 1\) introduces an uncertainty of about \(1/2\gamma^2\) or less than \(5\times 10^{-7}\).
The implementation of synchrotron radiation is not restricted to electrons and applies to any long lived charged particle including ions. The number of photons generated scales with the charge squared [Bur98]. The effects of synchrotron radiation from protons and ions are visible in the LHC and have been considered as source of background in FCC-hh studies [CBBK17]. The number of photons and the power scales with the square of the charge.
The standard synchrotron spectrum of Eq.(213) is only valid as long as the photon energy remains small compared to the particle energy [eal71, TEL82]. This is a very safe assumption for GeV electrons and standard magnets with fields of order of Tesla.
An extension of synchrotron radiation to fields exceeding several hundred Tesla, such as those present in the beam-beam interaction in linear-colliders, is also known as beamstrahlung. For an introduction see [Che86].
The standard photon spectrum applies to homogeneous fields and remains a good approximation for magnetic fields which remain approximately constant over a the length \(\rho/\gamma\), also known as the formation length for synchrotron radiation. Short magnets and edge fields will result instead in more energetic photons than predicted by the standard spectrum.
We also note that short bunches of many particles will start to radiate coherently like a single particle of the equivalent charge at wavelengths which are longer than the bunch dimensions.
Low energy, long-wavelength synchrotron radiation may destructively interfere with conducting surfaces [JBMG97].
The soft part of the synchrotron radiation spectrum emitted by charged particles travelling through a medium will be modified for frequencies close to and lower than the plasma frequency [Gri02].
Direct inversion and generation of the photon energy spectrum
The task is to find an algorithm that effectively transforms the flat distribution given by standard pseudo-random generators into the desired distribution proportional to the expressions given in Eqs.(213),(214). The transformation is obtained from the inverse \(F^{-1}\) of the cumulative distribution function \(F(x)=\int_0^x f(t) dt\).
Leaving aside constant factors, the probability density function relevant for the photon energy spectrum is
Numerical methods to evaluate \(K_{5/3}\) are discussed in [Luk75]. An efficient algorithm to evaluate the integral SynRad using Chebyshev polynomials is described in [HHUmstatter81]. This has been used in an earlier version of the Monte Carlo generator for synchrotron radiation using approximate transformations and the rejection method [Bur90].
The cumulative distribution function is the integral of the probability density function. Here we have
with normalization
such that \(\frac{3}{5\pi}{\rm SynRadInt}(x)\) gives the fraction of photons above \(x\).
It is possible to directly obtain the desired distribution with a fast and accurate algorithm using an analytical description based on simple transformations and Chebyshev polynomials. This approach is used here.
We now describe in some detail how the analytical description was obtained. For more details see [Bur].
It turned out to be convenient to start from the normalized complement rather then Eq.(215) directly, that is
which gives the fraction of photons below \(x\).
Fig. 60 shows \(y = {\rm SynFracInt(x)}\) and Fig. 61 the inverse \(x = {\rm InvSynFracInt}(y)\) together with simple approximate functions. We can see, that SynFracInt can be approximated by \(x^{1/3}\) for small arguments, and by \(1-e^{-x}\) for large \(x\). Consequently, we have for the inverse, \({\rm InvSynFracInt}(y)\), which can be approximated for small \(y\) by \(y^3\) and for large \(y\) by \(-\log(1-y)\).
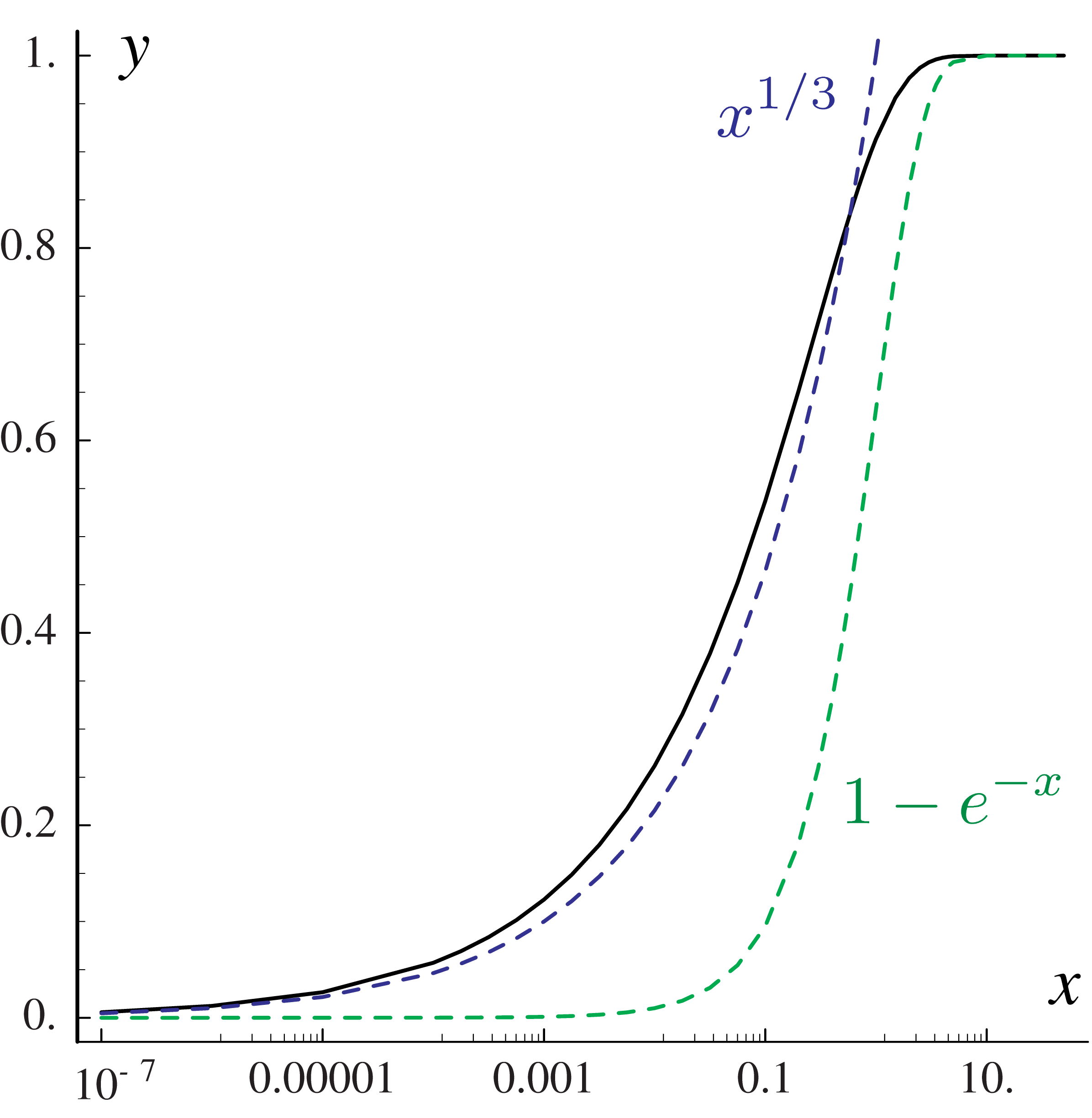
Fig. 60 SynFracInt on a log \(x\) scale. The functions \(x^{1/3}\), \(y^3\) and \(1-e^{-x}\), \(-\log(1-y)\) are shown as dashed lines.
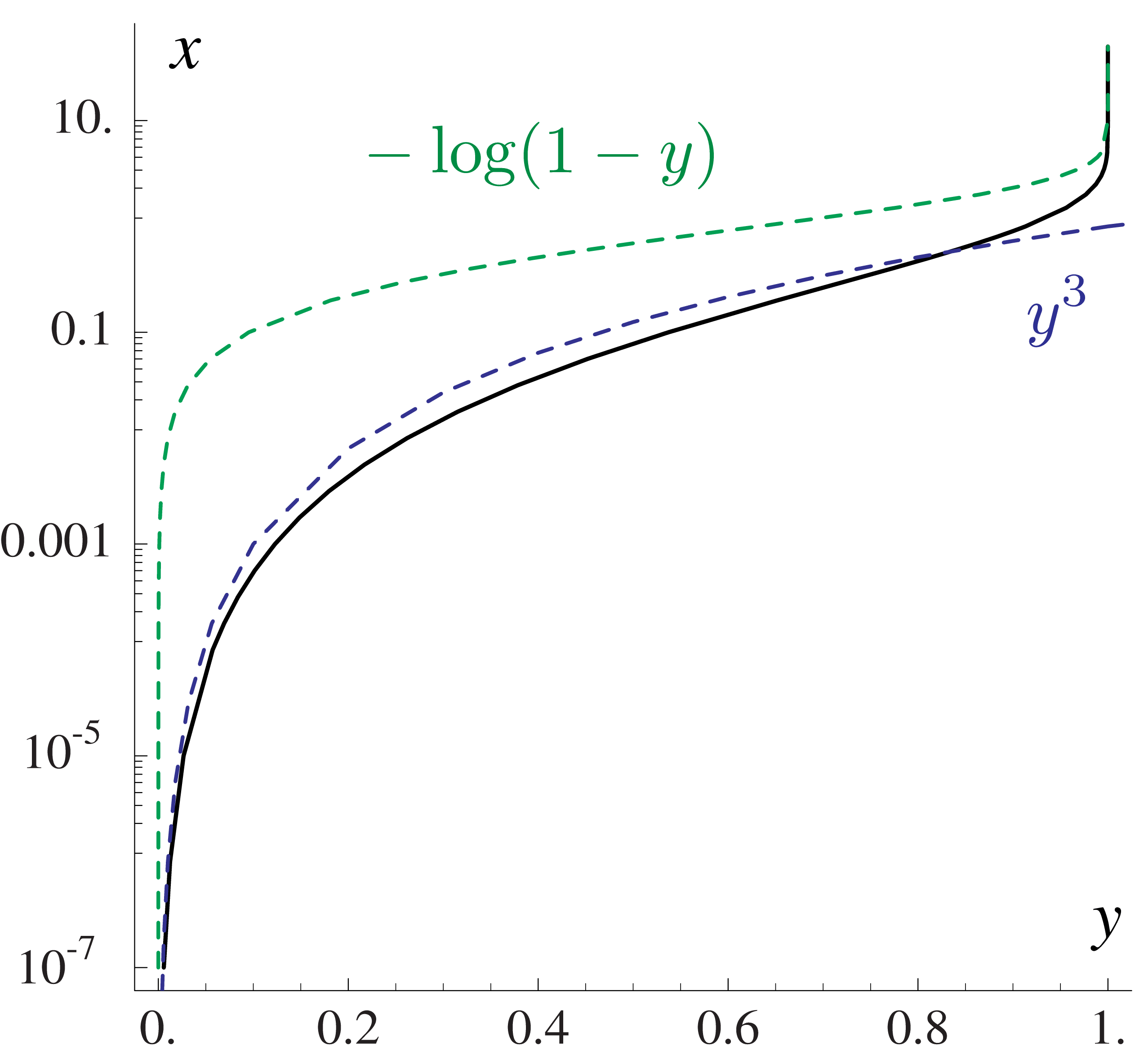
Fig. 61 InvSynFracInt on a log \(x\) scale. The functions \(x^{1/3}\), \(y^3\) and \(1-e^{-x}\), \(-\log(1-y)\) are shown as dashed lines.
Good convergence for \({\rm InvSynFracInt}(y)\) was obtained using Chebyshev polynomials combined with the approximate expressions for small and large arguments. For intermediate values, a Chebyshev polynomial can be used directly. Table 34 summarizes the expressions used in the different intervals.
\(y\) |
\(x={\rm InvSynFracInt}(y)\) |
|---|---|
\(y<0.7\) |
\(y^3 \, {\rm P}_{\rm Ch}(y)\) |
\(0.7 \leq y \leq 0.9999\) |
\({\rm P}_{\rm Ch}(y)\) |
\(y > 0.9999\) |
\(-\log(1-y) {\rm P}_{\rm Ch}(-\log(1-y))\) |
The procedure for Monte Carlo simulation is to generate \(y\) at random uniformly distributed between \(0\) at \(1\), as provided by standard random generators, and then to calculate the energy \(x\) in units of the critical energy according to \(x={\rm InvSynFracInt}(y)\).
The numerical accuracy of the energy spectrum presented here is about 14 decimal places, close to the machine precision. Fig. 62 shows a comparison of generated and expected spectra.
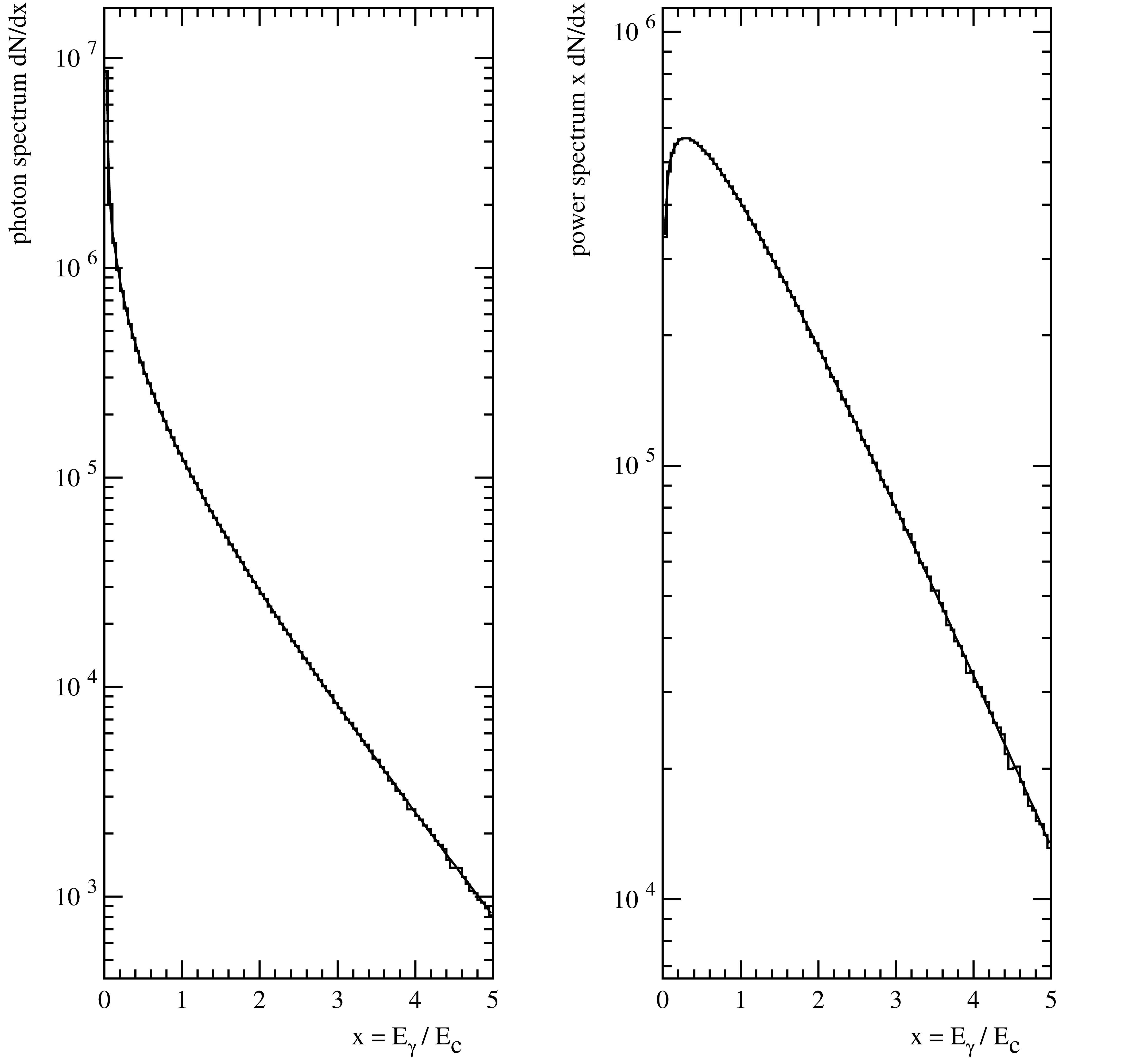
Fig. 62 Comparison of the exact (smooth curve) and generated (histogram) spectra for \(2\times 10^7\) events. The photon spectrum is shown on the left and the power spectrum on the right side.
A Geant4 display of an electron moving in a magnetic field radiating synchrotron photons is presented in Fig. 63.
Properties of the Power Spectra
The normalised probability function describing the photon energy spectrum is
\(n_\gamma(x)\) gives the fraction of photons in the interval \(x\) to \(x+dx\), where \(x\) is the photon energy in units of the critical energy. The first moment or mean value is
implying that the mean photon energy is \(\frac{8}{15\,\sqrt{3}} = 0.30792\) of the critical energy. The second moment about the mean, or variance, is
and the r.m.s. value of the photon energy spectrum is \(\sigma=\sqrt{\frac{211}{675}}=0.5591\).
The normalised power spectrum is
\(P_\gamma(x)\) gives the fraction of the power which is radiated in the interval \(x\) to \(x+dx\).
Half of the power is radiated below the critical energy
The mean value of the power spectrum is
The variance is
and the r.m.s. width is \(\sigma=\sqrt{\frac{2351}{1728}}=1.16642\).
Bibliography
- Bur
H. Burkhardt. Monte carlo generation of the energy spectrum of synchrotron radiation. CERN-AB and EuroTeV report. CERN-OPEN-2007-018. URL: http://cds.cern.ch/record/1038899.
- Bur98
H. Burkhardt. Reminder of the edge effect in synchrotron radiation. Technical Report 172, CERN, Geneva, 1998. LHC Project Note. URL: http://cds.cern.ch/record/692027.
- Bur90
H. Burkhardt. Monte carlo generator for synchrotron radiation. LEP Note 632, CERN, December 1990. URL: http://cds.cern.ch/record/443490.
- Che86
P. Chen. An introduction to beamstrahlung and disruption. Frontiers of Particle Beams, pages 481–494, Lecture Notes in Physics 296 1986. M. Month and S. Turner, eds. URL: http://slac.stanford.edu/pubs/slacpubs/4250/slac-pub-4379.pdf.
- CBBK17
F Collamati, M Boscolo, H Burkhardt, and R Kersevan. Synchrotron radiation backgrounds for the FCC-hh experiments. Journal of Physics: Conference Series, 874:012004, jul 2017. URL: https://doi.org/10.1088/1742-6596/874/1/012004.
- eal71
F. Herlach et al. Experiments with megagauss targets at slac. IEEE Trans. Nucl. Sci., NS 18(3):809–814, 1971. URL: https://doi.org/10.1109/TNS.1971.4326194.
- Gri02
V.M. Grichine. Radiation of accelerated charge in absorbing medium. CERN-OPEN-2002-056, 2002. URL: http://cds.cern.ch/record/582178.
- HHUmstatter81
H.H.Umstätter. CERN/PS/SM/81-13, CERN Geneva, 1981.
- Hof04
A. Hofmann. The Physics of Synchrotron Radiation. Cambridge University Press, edition, 2004.
- JBMG97
J.B. Murphy, S. Krinsky and R.L. Gluckstern. Longitudinal wakefield for an electron moving on a circular orbit. Part. Acc. 57, 9, 1997. URL: http://cds.cern.ch/record/1120287.
- JDJackson98
J.D.Jackson. Classical Electrodynamics. John Wiley and Sons, third edition, 1998.
- Luk75
Y. Luke. The special functions and their approximations. New York, NY: Academic Press, edition, 1975. 585p.
- ST86
A.A. Sokolov and I.M. Ternov. Radiation from Relativistic Electrons. Amer. Inst of Physics, edition, 1986.
- TEL82
D. White T. Erber, G.B. Baumgartner and H.G. Latal. Megagauss bremsstrahlung and radiation reaction. Batavia 1983, proceedings, High Energy Accelerators, pages 372–374, 1982. URL: https://inspirehep.net/files/8019a7defef117ad62cb1245ee9208f4.