Introduction

The ABLA++ evaporation model describes the de-excitation of hot remnants by taking their characteristic parameters, such as the excitation energy, mass number, atomic number and nucleus spin, as input. This model is a translation to C++ of the fortran code ABLA07 developed at GSI by Kelic and collaborators [KAH08]. Both codes contain the same physics and input parameters [RSCD+22], even if ABLA++ has been recently extended to the strange sector by including the emission of \(\Lambda\) particles and the formation of hypernuclei, see Refs. [RSDH+18] and [RSCD+23].

Evaporation

These models calculate the probabilities for emitting \(\gamma\mathrm{-rays}\), neutrons, light-charged particles, and intermediate-mass fragments (IMFs) according to Weisskopf’s formalism [WE40]. For a more realistic description of the deexcitation, the separation energies and the Coulomb barriers for charged particles are also considered according to the atomic mass evaluation AME 2020 [HWK+21] and the Bass potential [Bas80], respectively. In the case of hyper-remnants, the \(\Lambda\) separation energies are calculated according to the equation found by Samanta [SCB06].

The probabilities for emission of particle type \(j\) are calculated using formula``:

(269)\[W_j(N,Z,E) = \frac{\Gamma_j(N,Z,E)}{\sum_k\Gamma_k(N,Z,E)},\]

where \(\Gamma_j\) is emission width for particle \(j\), \(N\) is neutron number, \(Z\) charge number and \(E\) excitation energy. Possible emitted particles are \(\gamma\), \(n\), \(\Lambda\), \(p\), \(d\), \(t\), \({^3}He\), \(\alpha\) and IMFs. Emission widths are calculated using the following formula:

(270)\[\Gamma_j = \frac{1}{2 \pi \rho_c(E)} \frac{4 m_j R^2}{\hbar^2} T_j^2 \rho_j(E - S_j - B_j),\]

where \(\rho_c(E)\) and \(\rho_j(E - S_j - B_j)\) are the level densities of the compound nucleus and the exit channel, respectively. \(B_j\) is the height of the Coulomb barrier, \(S_j\) the separation energy, \(R\) is the radius and \(T_j\) the temperature of the remnant nucleus after emission and \(m_j\) the mass of the emitted particle. For \(\gamma\) emission, see Ref. [KAH08]. De-excitation by fission is also possible if the excitation energy is higher than the fission barrier height.

The summary of Geant4 ABLA++ implementation is represented in Table 54.

Table 54 ABLA++ (located in the Geant4 directory source/processes/hadronic/models/abla) feature summary.

Requirements
External data file	G4ABLA3.3 available at Geant4 site
Environment variable	G4ABLADATA
for external data
Usage
Physics list	No default physics list,
	see Section How to use ABLA++.
Interfaces
G4InclAblaCascadeInterface	h-A
G4InclAblaLightIonInterface	A-A
Supported input	Excited nuclei
Output particles	\(\gamma,\, n,\, \Lambda,\, p,\, d,\, t\), \({^3}He\), \(\alpha\)
	and IMFs (\(2 < Z < 6\))
	fission products
	residual nuclei
	multifragmentation products
	hyper-fission products and hyper-residues
Features	evaporation of \(\gamma,\, n,\, \Lambda,\, p,\, d,\, t\), \({^3}He\), \(\alpha\)
	intermediate-mass fragments (IMFs)
	fission and multifragmentation
Misc.	5 classes, \(\sim 12\mathrm{k}\) lines
	0.9 \(<\) speed C++/F77 \(<\) 1.1
References	Key reference: [RSCD+22], see also [KAH08]

Level densities

The nuclear level density is calculated according to the Fermi gas model as a funtion of the excitation energy \(E^{*}\) and the angular momentum \(J\), and is expressed as:

(271)\[\rho(E^{*},J)= \frac{J+1/2}{\sqrt{2\pi} \sigma^3} e^{- \frac{J(J+1)}{2\sigma^2} } \frac{\sqrt \pi}{12} \frac{e^S}{\widetilde{a}^{1/4} {E^{*}}^{5/4}}\]

where \(\sigma^2\) is the spin cut-off factor given by \(\sigma^2=\frac{\Im T}{\hbar^2}\) with \(\Im\) as the moment of inertia of the nucleus and \(T\) the nuclear temperture, \(E^{*}\) is the excitacion energy of the system, \(S\) is the entropy and \(\widetilde{a}\) is the level-density parameter in units of MeV \(^{-1}\). Generally, this last parameter can be written as:

(272)\[\widetilde{a}= \alpha_{v} A + \alpha_{s} B_{s} \cdot A^{2/3}+ \alpha_{k} B_{k} A^{1/3}\]

where A is the mass of the nucleus and \(\alpha_{v}\), \(\alpha_{s}\) and \(\alpha_{k}\) are the coefficients that correspond to the volume, surface and curvature components of the single-particle level densities, respectively. The values of these coefficients were calculated by Ignatyuk [Ign00] (\(\alpha_{v}=0.095\), \(\alpha_{s}=0.073\), and \(\alpha_{k}=0\) in units of MeV \(^{-1}\)) and are the most-frequently used in model calculations. In the equation, \(B_{s}\) represents the ratio between the surface of the deformed nucleus and a spherical nucleus while \(B_{k}\) corresponds to the ratio between the integrated curvature of the deformed nucleus and a spherical nucleus.

In order to account for the role of collective excitations in the decay of excited compound nuclei, the level density of Eq. (271) is corrected using the vibrational and rotational enhancement factors according to:

(273)\[\rho(E,J) = K_{vib} K_{rot} \rho(E,J)_{int}\]

where \(\rho(E,J)_{int}\) is given by Eq. (271), \(K_{vib}\) represents the vibrational enhancement factor and \(K_{rot}\) corresponds to the rotational factor. Both are calculated according to Ref. [JdJC+98].

Fission

The fission decay width is described by the Bohr-Wheeler transition-state model [BW39] following the formulation given by Moretto [Mor75]:

\[\Gamma_{f}^{BW}= \frac{T}{2 \pi} \frac{\rho_{sp}(E-B_f,J)}{\rho_{gs}(E,J)};\]

where \(\rho_{sp}(E-B_f,J)\) and \(\rho_{gs}(E,J)\) are the level densities at the saddle-point and ground-state configurations, respectively, and \(B_f\) is the fission-barrier height obtained from the finite-range liquid-drop model of Sierk [Sie86] taking into account the influence of angular momentum and considering the ground-state shell effects [MNMS95].

The diffussion process above the fission barrier is described by the Fokker-Planck equation, where the quasi- stationary solution of this equation was introduced by Kramers [Kra40] and provides a reduction of the fission decay width due to dissipation:

\[\Gamma_{f}^{K} = \left[ \sqrt{1+ \left(\frac{\beta}{2 \omega_{0}}\right)^2}-\frac{\beta}{2 \omega_{0}} \right] \Gamma_{f}^{BW}.\]

Here \(\beta\) is the reduced dissipation coefficient and \(\omega_{0}\) is the frequency of the harmonic oscillator describing the inverted potential at the fission barrier, calculated according to the liquid-drop model. This equation provides the asymptotic value of the fission decay width.

The analytical approximation to the solution of the one-dimensional Fokker-Planck equation for the time-dependent fission-decay width was developed by Jurado and collaborators in Refs. [JSB03, JSS+05], using a Gaussian distribution centred at the spherical shape as initial condition. The mean values and the widths of the initial Gaussian distributions in space and momentum are given by the entrance channel. In this approximation, the time-dependent fission-decay width is defined as:

\[\Gamma_f(t)= \frac{W_n (x = x_b ; t, \beta)}{W_n (x = x_b ; t\rightarrow \infty, \beta)} \Gamma_{f}^{K};\]

where W(x; t, \(\beta\)) is the normalized probability distribution at the saddle-point deformation \(x_b\). The saddle-point deformations are calculated according to Ref. [HM88].

The description of the properties of the fission fragments is based on a semi-empirical model developed in Refs. [BGdJ+98, KAB+02]. The fission channels are explained by the macroscopic and microscopic properties of the potential-energy landscape that is determined by the characteristics of the fissioning nucleus at the saddle point. In particular, the stiffness of the macroscopic potential along the mass-asymmetry degree of freedom is obtained from the systematics of the width of mass distributions measured in Ref. [RIO97]. The neutron-to-proton ratio (N/Z) of the fission fragments is assumed to be given by the unchanged-charge distribution (UCD). This (N/Z) ratio is modified by the charge polarization effect calculated in terms of the liquid-drop model (LDM) by assuming a two touching spheres configuration at the scission point, and by the evaporation of particles during the descent from saddle to scission [RSCD+22]. Finally, at the scission point, the two fission fragments are characterized by their atomic numbers \(Z_{1,2}\), mass numbers \(A_{1,2}\), kinetic energies \(E_{kin}^{1,2}\), and excitation energies \(E_{exc}^{1,2}\). After the formation of the two fission fragments, their corresponding deexcitation chains are followed until their excitation energies fall below the lowest particle-emission threshold.

According to the statistical model, the widths of the mass and atomic-number distributions of the fission fragments (\(\sigma_A\) and \(\sigma_Z\) respectively) are related to the temperature at the saddle point, following the equations:

(274)\[\sigma_A^2 = \frac{A^2_{fiss}T_{sad}}{16d^2V/d\nu^2} \; \; and \; \; \sigma_Z^2 = \frac{Z^2_{fiss}T_{sad}}{16d^2V/d\nu^2}\]

where \(d^2 V/d \nu^2\) is the second derivative of the potential with respect to the mass-asymmetry degree of freedom at the saddle point \(\nu= (4/A_{fiss} )/(M-A_{fiss}/2)\). \(A_{fiss}\) and \(Z_{fiss}\) correspond to the mass and atomic numbers of the fissioning nucleus, respectively, and M represents the mass number of the corresponding fragment.

The kinetic energies of the fission fragments are calculated according to the semi-statistical scission point model of Wilkins and collaborators [WSC76]. The main contribution to the total kinetic energies released in the fission process comes from the Coulomb repulsion of the two fission fragments at the scission point and, therefore, this total kinetic energy is given by:

(275)\[TKE \sim \frac{ Z_1 Z_2}{D}\]

where \(Z_1\) and \(Z_2\) refer to the atomic number of the two fission fragments, and \(D\) is the distance between the two uniformly-charged spheroids representing the fission fragments. This distance is parametrized as:

(276)\[D = r_0 A_1^{*1/3} \left( 1+\frac{2\beta_1}{3} \right) + r_0 A_2^{*1/3} \left(1+\frac{2\beta_2}{3} \right)+d\]

where \(A_1^*\) and \(A_2^*\) refer to the mass number of the two fission fragments at the scission point, \(\beta_1\) and \(\beta_2\) are their quadrupole deformations at the scission point, \(r_0\) is the fermi radius, and \(d\) is the distance between the tips of the two fission fragments. Here, we take \(d\) = 2 fm.

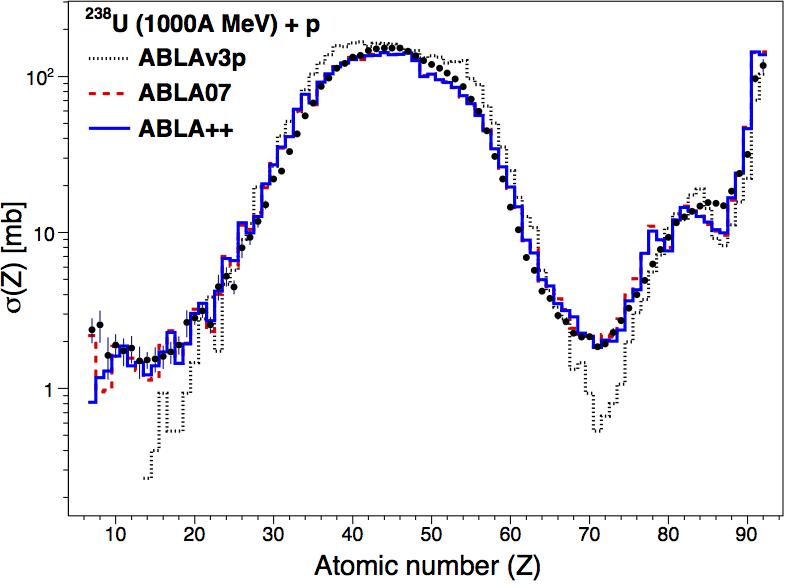
Fig. 116 ABLA calculations performed with the fortran version (ABLA07), the new one in C++ (ABLA++) and the previous version (ABLAv3p) are compared with the atomic-number distribution of fission and evaporation residues produced in the reactions p + \(^{238}\mathrm{U}\) at 1A GeV.

Multifragmentation

If the excitation energy acquired during the first, collision, stage is high enough, the increase of volume has a dramatic consequence: The nucleus enters the spinodal region [CCR04] characterized by negative incompressibility. In this region, an increase in the system volume due to expansion is connected with the increase in pressure, and, consequently, any local fluctuation in density is strongly amplified leading to a mixed phase consisting of droplets represented by a small amount of light nuclei at normal nuclear density, and the nuclear gas represented by individual nucleons. This process is often called “break-up”. The fragments formed in this process undergo deexcitation process and cool down. What is finally experimentally observed are the cold fragments, normally called IMFs. The entire multifragmentation process is scientifically very interesting for its relation to the equation-of-state of nuclear matter, in particular to the liquid-gas phase transition.

The starting point of the multifragmentation stage in ABLA++ is a hot nuclear system –so-called “spectator”, leftover of the initial collision stage. We assume that, if the excitation energy per nucleon of the spectator exceeds a limiting value [KAH08], the system undergoes the break-up stage; otherwise we assume that it will directly de-excite through sequential evaporation and/or fission.

About the limiting excitation energy per nucleon, two options are possible in ABLA++. The default option is a mass-dependent value of the limiting excitation energy, deduced from the mass dependence of the temperature in the plateau of the caloric curve as pointed out by Natowitz in [NWH+02]. Another possible option is to assume that the limiting excitation energy per nucleon is constant for all nuclei; its value is fixed to 5.5 MeV.

The comparison of the new version of ABLA07 in C++ with the previous versions is shown in Fig. 116 for the reaction p + \(^{238}\mathrm{U}\) at 1A GeV. The calculations are also compared with the experimental data obtained at GSI [RAB+06]. This benchmark demonstrates that the new version ABLA++ reproduces the results obtained with the fortran code and confirms also the improvement with respect to the old version ABLAv3p.

External data file required

ABLA++ needs specific data files. These files contain ABLA++ shell corrections and nuclear masses. To enable this data set, the environment variable G4ABLADATA needs to be set, and the relevant data should be installed on your machine. You can download them from the Geant4 web site or you can have CMake download them for you during installation. For Geant4 11.2 we use the G4ABLA3.3 data files.

How to use ABLA++

None of the stock physics lists use the ABLA++ model by default. It should also be understood that ABLA++ is a nuclear de-excitation model and must be used as a secondary reaction stage; the first, dynamical reaction stage must be simulated using some other model, typically an intranuclear-cascade (INC) model. The coupling of the ABLA++ to the INCL++ model (Chapter INCL++: the Liège Intranuclear Cascade Model) has been somewhat tested and seems to work, but no extensive benchmarking has been realized at the time of writing. Coupling to the Binary-Cascade model (Chapter The Binary Cascade Model) should in principle be possible, but has never been tested. The technique to realize the coupling is described in the Application Developer Guide.

Bibliography

Bas80

R. Bass. Fusion reactions: successes and limitations of a one-dimensional description. Proceedings of the Symposium on Deep-Inelastic and Fusion Reactions with Heavy Ions, Springer Verlag, Berlin, 1980, pages 281–293, 1980.

BGdJ+98

J. Benlliure, A. Grewe, M. de Jong, K.-H. Schmidt, and S. Zhdanov. Calculated nuclide production yields in relativistic collisions of fissile nuclei. Nuclear Physics A, 628(3):458 – 478, 1998. URL: http://www.sciencedirect.com/science/article/pii/S0375947497006076, doi:https://doi.org/10.1016/S0375-9474(97)00607-6.

BW39

Niels Bohr and John Archibald Wheeler. The mechanism of nuclear fission. Physical Review, 56(5):426–450, Sep 1939. URL: https://doi.org/10.1103/PhysRev.56.426, doi:10.1103/physrev.56.426.

CCR04

Philippe Chomaz, Maria Colonna, and Jørgen Randrup. Nuclear spinodal fragmentation. Physics Reports, 389(5):263 – 440, 2004. URL: http://www.sciencedirect.com/science/article/pii/S0370157303003934, doi:https://doi.org/10.1016/j.physrep.2003.09.006.

HM88

Rainer W. Hasse and William D. Myers. Folded Distributions, pages 25–28. Springer Berlin Heidelberg, Berlin, Heidelberg, 1988. URL: https://doi.org/10.1007/978-3-642-83017-4_3, doi:10.1007/978-3-642-83017-4_3.

HWK+21

W.J. Huang, Meng Wang, F.G. Kondev, G. Audi, and S. Naimi. The ame 2020 atomic mass evaluation: (i). evaluation of input data, adjustment procedures. Chinese Physics C, 45(3):030002, 2021. URL: https://dx.doi.org/10.1088/1674-1137/abddb0, doi:10.1088/1674-1137/abddb0.

Ign00

A. V. Ignatyuk. Systematics of low-lying level densities and radiative widths. Proceedings of the Conference Bologna 2000: Structure of the Nucleus at the Dawn of the Century, Bologna, Italy, 29 May - 3 June 2000, edited by G. C. Bonsignori, M. Bruno, A. Ventura, and D. Vretenar, pages 287–292, 2000.

JdJC+98

A.R. Junghans, M. de Jong, H.-G. Clerc, A.V. Ignatyuk, G.A. Kudyaev, and K.-H. Schmidt. Projectile-fragment yields as a probe for the collective enhancement in the nuclear level density. Nuclear Physics A, 629(3):635 – 655, 1998. URL: http://www.sciencedirect.com/science/article/pii/S0375947498006587, doi:https://doi.org/10.1016/S0375-9474(98)00658-7.

JSB03

B. Jurado, K.-H. Schmidt, and J. Benlliure. Time evolution of the fission-decay width under the influence of dissipation. Physics Letters B, 553(3):186 – 190, 2003. URL: http://www.sciencedirect.com/science/article/pii/S0370269302032343, doi:https://doi.org/10.1016/S0370-2693(02)03234-3.

JSS+05

B. Jurado, C. Schmitt, K.-H. Schmidt, J. Benlliure, and A.R. Junghans. A critical analysis of the modelling of dissipation in fission. Nuclear Physics A, 747(1):14 – 43, 2005. URL: http://www.sciencedirect.com/science/article/pii/S0375947404010759, doi:https://doi.org/10.1016/j.nuclphysa.2004.09.123.

KAH08(1,2,3,4,5)

Ricciardi M V Kelic A and Schmidt K H. Abla07 — towards a complete description of the decay channels of a nuclear system from spontaneous fission to multifragmentation. In D Filges, S Leray, Y Yariv, A Mengoni, A Stanculescu, and G Mank Eds., editors, Proceedings of the Joint ICTP-IAEA Advanced Workshop on Model Codes for Spallation Reactions, number INDC(NDS)-530, 181. ICTP Trieste, Italy, 4-8 February 2008. IAEA, IAEA Vienna, August 2008. download: https://www-nds.iaea.org/publications/indc/indc-nds-0530.pdf.

Kra40

H.A. Kramers. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica, 7(4):284 – 304, 1940. URL: http://www.sciencedirect.com/science/article/pii/S0031891440900982, doi:https://doi.org/10.1016/S0031-8914(40)90098-2.

KAB+02

K. Kruglov, A. Andreyev, B. Bruyneel, S. Dean, S. Franchoo, M. Górska, K. Helariutta, M. Huyse, Yu. Kudryavtsev, W.F. Mueller, N.V.S.V. Prasad, R. Raabe, K.-H. Schmidt, P. Van Duppen, J. Van Roosbroeck, K. Van de Vel, and L. Weissman. Yields of neutron-rich isotopes around z = 28 produced in 30 mev proton-induced fission of 238u. The European Physical Journal A - Hadrons and Nuclei, 14(3):365–370, Jul 2002. URL: https://doi.org/10.1140/epja/i2002-10013-1, doi:10.1140/epja/i2002-10013-1.

MNMS95

P. Moller, J.R. Nix, W.D. Myers, and W.J. Swiatecki. Nuclear ground-state masses and deformations. Atomic Data and Nuclear Data Tables, 59(2):185 – 381, 1995. URL: http://www.sciencedirect.com/science/article/pii/S0092640X85710029, doi:https://doi.org/10.1006/adnd.1995.1002.

Mor75

Luciano G. Moretto. Statistical emission of large fragments: a general theoretical approach. Nuclear Physics A, 247(2):211 – 230, 1975. URL: http://www.sciencedirect.com/science/article/pii/0375947475906326, doi:https://doi.org/10.1016/0375-9474(75)90632-6.

NWH+02

J. B. Natowitz, R. Wada, K. Hagel, T. Keutgen, M. Murray, A. Makeev, L. Qin, P. Smith, and C. Hamilton. Caloric curves and critical behavior in nuclei. Phys. Rev. C, 65:034618, Mar 2002. URL: https://link.aps.org/doi/10.1103/PhysRevC.65.034618, doi:10.1103/PhysRevC.65.034618.

RAB+06

M. V. Ricciardi, P. Armbruster, J. Benlliure, M. Bernas, A. Boudard, S. Czajkowski, T. Enqvist, A. Kelić, S. Leray, R. Legrain, B. Mustapha, J. Pereira, F. Rejmund, K.-H. Schmidt, C. Stéphan, L. Tassan-Got, C. Volant, and O. Yordanov. Light nuclides produced in the proton-induced spallation of \(^2\)\(^3\)\(^8\)U at 1 GeV. Physical Review C, January 2006. URL: http://dx.doi.org/10.1103/PhysRevC.73.014607, doi:10.1103/physrevc.73.014607.

RSCD+22(1,2,3,4)

J. L. Rodriguez-Sanchez, J. Cugnon, J.-C. David, J. Hirtz, A. Kelić-Heil, and S. Leray. Hypernuclei formation in spallation reactions by coupling the liège intranuclear cascade model to the deexcitation code abla. Physical Review C, Jan 2022. URL: https://doi.org/10.1103/PhysRevC.105.014623, doi:10.1103/physrevc.105.014623.

RSCD+23

J. L. Rodriguez-Sanchez, J. Cugnon, J.-C. David, J. Hirtz, A. Kelić-Heil, and I. Vidaña. Constraint of the nuclear dissipation coefficient in fission of hypernuclei. Physical Review Letter, Mar 2023. URL: https://link.aps.org/doi/10.1103/PhysRevLett.130.132501, doi:10.1103/PhysRevLett.130.132501.

RSDH+18

Jose Luis Rodriguez-Sanchez, Jean-Christophe David, Jason Hirtz, Joseph Cugnon, and Sylvie Leray. Constraining the Λ-nucleus potential within the liège intranuclear cascade model. Physical Review C, Aug 2018. URL: https://doi.org/10.1103/PhysRevC.98.021602, doi:10.1103/physrevc.98.021602.

RIO97

A. Ya. Rusanov, M. G. Itkis, and V. N. Okolovic. Mass distribution properties of fission fragments of hot rotating nuclei. Physics of Atomic Nuclei, 60():683, 1997.

SCB06

C. Samanta, P. Roy Chowdhury, and D. N. Basu. Generalized mass formula for non-strange and hypernuclei with su(6) symmetry breaking. Journal of Physics G: Nuclear and Particle Physics, Feb 2006. URL: https://doi.org/10.1088/0954-3899/32/3/010, doi:10.1088/0954-3899/32/3/010.

Sie86

Arnold J. Sierk. Macroscopic model of rotating nuclei. Phys. Rev. C, 33:2039–2053, Jun 1986. URL: https://link.aps.org/doi/10.1103/PhysRevC.33.2039, doi:10.1103/PhysRevC.33.2039.

WE40

V. F. Weisskopf and D. H. Ewing. On the yield of nuclear reactions with heavy elements. Physical Review, 57(6):472–485, Mar 1940. URL: https://doi.org/10.1103/PhysRev.57.472, doi:10.1103/physrev.57.472.

WSC76

B. D. Wilkins, E. P. Steinberg, and R. R. Chasman. Scission-point model of nuclear fission based on deformed-shell effects. Phys. Rev. C, 14:1832–1863, Nov 1976. URL: https://link.aps.org/doi/10.1103/PhysRevC.14.1832, doi:10.1103/PhysRevC.14.1832.