Introduction

This cascade model is a re-engineered version of the INUCL code and includes the Bertini intra-nuclear cascade model with excitons, a pre-equilibrium model, a nucleus explosion model, a fission model, and an evaporation model. It treats nuclear reactions initiated by long-lived hadrons (\(p, n, \pi, K, \Lambda, \Sigma, \Xi , \Omega\)) and \(\gamma\)s with energies between 0 and 10 GeV. Presented here is an overview of the models and a review of results achieved from simulations and comparisons with experimental data.

The intranuclear cascade model (INC) was was first proposed by Serber in 1947 [Ser47]. He noticed that in particle-nuclear collisions the deBroglie wavelength of the incident particle is comparable (or shorter) than the average intra-nucleon distance. Hence, a description of interactions in terms of particle-particle collisions is justified.

The INC has been used succesfully in Monte Carlo simulations at intermediate energies since Goldberger made the first hand-calculations in 1947 [Gol48]. The first computer simulations were done by Metropolis et al. in 1958 [MBS58]. Standard methods in INC implementations were developed when Bertini published his results in 1968 [GAB68]. An important addition to INC was the exciton model introduced by Griffin in 1966 [Gri66].

The current presentation describes the implementation of the Bertini INC model within the Geant4 hadronic physics framework [eal03]. This framework is flexible and allows for the modular implementation of various kinds of hadronic interactions.

The Geant4 Cascade Model

Inelastic particle-nucleus collisions are characterized by both fast and slow components. The fast (10^-23 - 10^-22 s) intra-nuclear cascade results in a highly excited nucleus which may decay by fission or pre-equilibrium emission. The slower (10^-18 - 10^-16 s) compound nucleus phase follows with evaporation. A Boltzmann equation must be solved to treat the collision process in detail.

The intranuclear cascade (INC) model developed by Bertini [BG71, GAB68] solves the Boltzmann equation on average. This model has been implemented in several codes such as HETC [AAH90]. Our model, which is based on a re-engineering of the INUCL code [eal99], includes the Bertini intranuclear cascade model with excitons, a pre-equilibrium model, a simple nucleus explosion model, a fission model, and an evaporation model.

The target nucleus is modeled by up to six concentric shells of constant density as an approximation to the continuously changing density distribution of nuclear matter within nuclei. The cascade begins when an incident particle strikes a nucleon in the target nucleus and produces secondaries. The secondaries may in turn interact with other nucleons or be absorbed. The cascade ends when all particles, which are kinematically able to do so, escape the nucleus. At that point energy conservation is checked. Relativistic kinematics is applied throughout the cascade.

Model Limits

The model is valid for incident \(p, n, \pi, K, \Lambda, \Sigma, \Xi , \Omega\) and \(\gamma\)s with energies between 0 and 10 GeV. All types of nuclear targets are allowed.

The necessary condition of validity of the INC model is \(\lambda_{B} / v \ll \tau_{c} \ll \Delta t\), where \(\delta_{B}\) is the deBroglie wavelenth of the nucleons, \(v\) is the average relative velocity between two nucleons and \(\Delta t\) is the time interval between collisions. At energies below 200 MeV, this condition is no longer strictly valid, and a pre-quilibrium model must be invoked. At energies greater than ~10 GeV the INC picture breaks down. This model has been tested against experimental data at incident kinetic energies between 100 MeV and 10 GeV.

Intranuclear Cascade Model

The basic steps of the INC model are summarized as follows:

the space point at which the incident particle enters the nucleus is selected uniformly over the projected area of the nucleus,
the total particle-particle cross sections and region-depenent nucleon densities are used to select a path length for the projectile,
the momentum of the struck nucleon, the type of reaction and the four-momenta of the reaction products are determined, and
the exciton model is updated as the cascade proceeds.
If the Pauli exclusion principle allows and \(E_{particle} > E_{cutoff}\) = 2 MeV, step (2) is performed to transport the products.

After the intra-nuclear cascade, the residual excitation energy of the resulting nucleus is used as input for non-equilibrium model.

Nuclear Model

Some of the basic features of the nuclear model are:

the nucleons are assumed to have a Fermi gas momentum distribution. The Fermi energy is calculated in a local density approximation i.e. the Fermi energy is made radius-dependent with Fermi momentum \(p_{F}(r) = (\frac{3 \pi^2 \rho(r)}{2})^\frac{1}{3}\).
Nucleon binding energies (BE) are calculated using the mass formula. A parameterization of the nuclear binding energy uses a combination of the Kummel mass formula and experimental data. Also, the asymptotic high temperature mass formula is used if it is impossible to use experimental data.

Initialization

The initialization phase fixes the nuclear radius and momentum according to the Fermi gas model.

If the target is hydrogen (A = 1) a direct particle-particle collision is performed, and no nuclear modeling is required.

If \(1 < A < 4\), a nuclear model consisting of one layer with a radius of 8.0 fm is created.

For \(4 < A < 11\), the nuclear model is composed of three concentric spheres \(i = \{1, 2, 3\}\) with radius

\[r_{i}(\alpha_{i}) = \sqrt{C_{1}^{2} \left(1 - \frac{1}{A}\right) + 6.4} \sqrt{-\log( \alpha_{i})}.\]

Here \(\alpha_{i} = \{0.01, 0.3, 0.7\}\) and \(C_{1} = 3.3836 A^{1/3}\).

If \(A > 11\), a nuclear model with three concentric spheres is also used. The sphere radius is now defined as

\[r_{i}(\alpha_{i}) = C_{2} \log \left({\frac{1 + e^{- \frac{C_{1}}{C_{2}}}} {\alpha_{i}} - 1} \right) + C_{1} ,\]

where \(C_{2} = 1.7234\).

The potential energy \(V\) for nucleon \(N\) is

\[V_{N} = \frac{p_{F}^2}{2 m_{N}} + BE_{N}(A, Z) ,\]

where \(p_f\) is the Fermi momentum and \(BE\) is the binding energy.

The momentum distribution in each region follows the Fermi distribution with zero temperature.

\[f(p) = c p ^2\]

where

\[\int_0^{p_F} f(p) dp = n_{p} \mbox{ or } n_{n}\]

where \(n_p\) and \(n_n\) are the number of protons or neutrons in the region. \(P_f\) is the momentum corresponding to the Fermi energy

\[E_f = \frac{p_F^2}{2 m_N} = \frac{\hbar^2}{2 m_N} \left( \frac{3 \pi^2}{v} \right)^{2/3} ,\]

which depends on the density \(n/v\) of particles, and which is different for each particle and each region.

Pauli Exclusion Principle

The Pauli exclusion principle forbids interactions where the products would be in occupied states. Following the assumption of a completely degenerate Fermi gas, the levels are filled from the lowest level. The minimum energy allowed for the products of a collision correspond to the lowest unfilled level of the system, which is the Fermi energy in the region. So in practice, the Pauli exclusion principle is taken into account by accepting only secondary nucleons which have \(E_N > E_f\).

Cross Sections and Kinematics

Path lengths of nucleons in the nucleus are sampled according to the local density and the free \(N-N\) cross sections. Angles after the collision are sampled from experimental differential cross sections. Tabulated total reaction cross sections are calculated by Letaw’s formulation [eal83, eal93, Pea89]. For \(N-N\) cross sections the parameterizations are based on the experimental energy and isospin dependent data. The parameterization described in [BT72] is used.

For pions the intra-nuclear cross sections are provided to treat elastic collisions and the following inelastic channels: \(\pi^{-}\)p \(\rightarrow\) \(\pi^{0}\)n, \(\pi^{0}\)p \(\rightarrow\) \(\pi^{+}\)n, \(\pi^{0}\)n \(\rightarrow\) \(\pi^{-}\)p, and \(\pi^+\)n \(\rightarrow\) \(\pi^0\)p. Multiple particle production is also implemented.

The pion absorption channels are \(\pi^{+}\)nn \(\rightarrow\) pn, \(\pi^{+}\)pn \(\rightarrow\) pp, \(\pi^{0}\)nn \(\rightarrow\) nn, \(\pi^{0}\)pn \(\rightarrow\) pn, \(\pi^{0}\)pp \(\rightarrow\) pp, \(\pi^{-}\)pn \(\rightarrow\) nn , and \(\pi^{-}\)pp \(\rightarrow\) pn.

Pre-equilibrium Model

The Geant4 cascade model implements the exciton model proposed by Griffin [Gri66, Gri67]. In this model, nucleon states are characterized by the number of excited particles and holes (the excitons). Intra-nuclear cascade collisions give rise to a sequence of states characterized by increasing exciton number, eventually leading to an equilibrated nucleus. For a practical implementation of the exciton model we use parameters from [eal73], (level densities) and [Kal78] (matrix elements).

In the exciton model the possible selection rules for particle-hole configurations in the source of the cascade are: \(\Delta p = 0, \pm 1\) \(\Delta h = 0, \pm 1\) \(\Delta n = 0, \pm 2\), where \(p\) is the number of particles, \(h\) is number of holes and \(n = p + h\) is the number of excitons.

The cascade pre-equilibrium model uses target excitation data and the exciton configurations for neutrons and protons to produce non-equilibrium evaporation. The angular distribution is isotropic in the rest frame of the exciton system.

Parameterizations of the level density are tabulated as functions of \(A\) and \(Z\), and with high temperature behavior (the nuclear binding energy using the smooth liquid high energy formula).

Break-up models

Fermi break-up is allowed only in some extreme cases, i.e. for light nuclei (\(A < 12\) and \(3 (A - Z) < Z < 6\) ) and \(E_{excitation} > 3 E_{binding}\). A simple explosion model decays the nucleus into neutrons and protons and decreases exotic evaporation processes.

The fission model is phenomenological, using potential minimization. A binding energy paramerization is used and some features of the fission statistical model are incorporated [Fon69].

Evaporation Model

A statistical theory for particle emission of the excited nucleus remaining after the intra-nuclear cascade was originally developed by Weisskopf [Wei37]. This model assumes complete energy equilibration before particle emission, and re-equilibration of excitation energies between successive evaporations. As a result the angular distribution of emitted particles is isotropic.

The Geant4 evaporation model for the cascade implementation adapts the often-used computational method developed by Dostrowski [DFF59, DFR60]. The emission of particles is computed until the excitation energy falls below some specific cutoff. If a light nucleus is highly excited, the Fermi break-up model is executed. Also, fission is performed if that channel is open. The main chain of evaporation is followed until \(E_{excitation}\) falls below E\(_{cutoff}\) = 0.1 MeV. The evaporation model ends with an emission chain which is followed until \(E_{excitation} < E^{\gamma}_{cutoff} = 10^{-15}\) MeV.

An example of Bertini evaporation model in action is shown in Fig. 99.

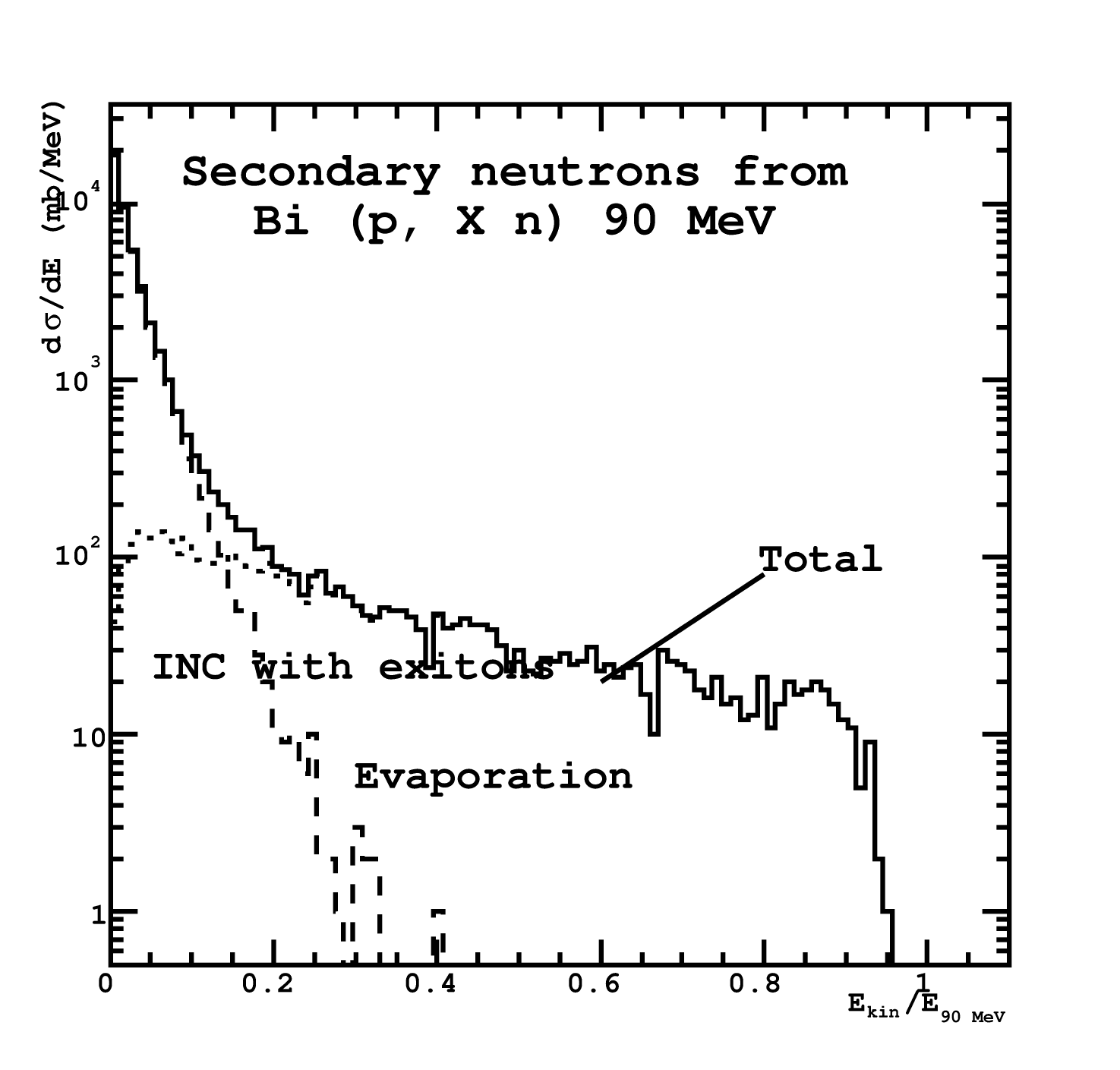
Fig. 99 Secondary neutrons generated by Bertini INC with excitons and evaporation model.

Interfacing Bertini implementation

Typically Bertini models are used through physics lists, with ’BERT’ in their name. User should consult these validated physics model collection to understand the inclusion mechanisms before using directly the actual Bertini cascade interfaces:

G4CascadeInterface: All the Bertini cascade submodels in integrated fashion, can be used collectively through this interface using method ApplyYourself. A Geant4 track (G4Track) and a nucleus (G4Nucleus) are given as parameters.
G4ElasticCascadeInterface: provides an access to elastic hadronic scattering. Particle treated are the same as in case for G4CascadeInterface but only elastic scattering is modeled.
G4PreCompoundCascadeInterface: provides an interface to INUCL intra nuclear cascade with excitons. Subsequent evaporation phase is not modeled.
G4InuclEvaporation: provides an interface to INUCL evaporation model. This interface with method BreakItUp inputs an excited nuclei G4Fragment to model evaporation phase.

Bibliography

AAH90: R.G. Alsmiller, F.S. Alsmiller, and O.W. Hermann. The high-energy transport code hetc88 and comparisons with experimental data. Nuclear Instruments and Methods in Physics Research A, 295():337–343, 1990.
BT72: V.S. Barashenkov and V.D. Toneev. High Energy interactions of particles and nuclei with nuclei (In russian). 1972.
BG71: H. W. Bertini and P. Guthrie. Results from medium-energy intranuclear-cascade calculation. Nucl. Phys. A, 1971.
DFF59: I. Dostrovsky, Z. Fraenkel, and G. Friedlander. Monte carlo calculations of nuclear evaporation processes. III. applications to low-energy reactions. Physical Review, 116(3):683–702, Nov 1959. URL: https://doi.org/10.1103/PhysRev.116.683, doi:10.1103/physrev.116.683.
DFR60: I. Dostrovsky, Z. Fraenkel, and P. Rabinowitz. Monte carlo calculations of nuclear evaporation processes. v. emission of particles heavier than \(^4\)He. Physical Review, 118(3):791–793, May 1960. URL: https://doi.org/10.1103/physrev.118.791, doi:10.1103/physrev.118.791.
eal73: I. Ribansky et al. Pre-equilibrium decay and the exciton model. Nucl. Phys. A, 205():545–560, 1973.
eal83: J. R. Letaw et al. The Astrophysical Journal Supplements, 51:271, 1983.
eal93: J. R. Letaw et al. The Astrophysical Journal, 414:601, 1993.
eal03: S. Agostinelli et al. Geant4—a simulation toolkit. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 506(3):250–303, Jul 2003. URL: https://doi.org/10.1016/S0168-9002(03)01368-8, doi:10.1016/s0168-9002(03)01368-8.
eal99: Yu. E. Titarenko et al. Experimental and computer simulations study of radionuclide production in heavy materials irradiated by intermediate energy protons. Technical Report nucl-ex/9908012, pre-print, 1999.
Fon69: P. Fong. Statistical Theory of Fission. Gordon and Breach, New York, 1969.
Gol48: M. Goldberger. The interaction of high energy neutrons and hevy nuclei. Phys. Rev., 74:1269, 1948.
Gri66(1,2): J. J. Griffin. Statistical model of intermediate structure. Physical Review Letters, 17():478–481, 1966.
Gri67: J. J. Griffin. Statistical model of intermediate structure. Physical Letters, 24B(1):5–7, 1967.
GAB68(1,2): M. P. Guthrie, R. G. Alsmiller, and H. W. Bertini. Nucl. Instr. Meth., 66:29, 1968.
Kal78: C. Kalbach. Exciton number dependence of the griffin model two-body matrix element. Z. Physik A, 287:319–322, 1978.
MBS58: N. Metropolis, R. Bibins, and M. Storm. Monte carlo calculations on intranuclear cascades. i. low-energy studies. Physical Review, 110:185, 1958.
Pea89: S. Pearlstein. Medium-energy nuclear data libraries: a case study, neutron- and proton-induced reactions in \(^5\)\(^6\)Fe. The Astrophysical Journal, 346():1049–1060, 1989.
Ser47: R. Serber. Nuclear reactions at high energies. Phys. Rev., 72:1114, 1947.
Wei37: V. Weisskopf. Statistics and nuclear reactions. Physical Review, 52(4):295–303, Aug 1937. URL: https://doi.org/10.1103/PhysRev.52.295, doi:10.1103/physrev.52.295.