Method of Calculation

The Glauber model [Gla70] is used as an alternative method of calculating differential cross sections for elastic and quasi-elastic hadron-nucleus scattering at high and intermediate energies.

For high energies this includes corrections for inelastic screening and for quasi-elastic scattering the exitation of a discrete level or a state in the continuum is considered.

The usual expression for the Glauber model amplitude for multiple scattering was used

(220)\[F(q)=\frac{ik}{2\pi} \int d^2{b}e^{\vec{\mathstrut q} \cdot \vec{\mathstrut b}} M(\vec b) .\]

Here \(M(\vec b)\) is the hadron-nucleus amplitude in the impact parameter representation

(221)\[M(\vec b) = 1- \left[1-e^{-A\int d^{3}r\Gamma(\vec{\mathstrut b}- \vec{\mathstrut s})\rho(\vec {r})} \right]^A,\]

\(k\) is the incident particle momentum, \(\vec q = \vec k' - \vec k\) is the momentum transfer, and \(\vec k'\) is the scattered particle momentum. Note that \(\left| \vec q \right| ^2 = -t\) - invariant momentum transfer squared in the center of mass system. \(\Gamma(\vec {b})\) is the hadron-nucleon amplitude of elastic scattering in the impact-parameter representation

(222)\[\Gamma(\vec b)=\frac{\displaystyle 1} {\displaystyle 2\pi ik^{hN}} \int d\vec {q} e^{-\vec {\mathstrut q} \cdot \vec{\mathstrut b}} f(\vec {q}).\]

The exponential parameterization of the hadron-nucleon amplitude is usually used:

(223)\[f(\vec {q})=\frac{\displaystyle ik^{hN}\sigma^{hN}}{2\pi} e^{-0.5q^2B}.\]

Here \(\sigma^{hN}=\sigma_{tot}^{hN}(1-i\alpha) \sigma_{tot}^{hN}\) is the total cross section of a hadron-nucleon scattering, \(B\) is the slope of the diffraction cone and \(\alpha\) is the ratio of the real to imaginary parts of the amplitude at \(q=0\). The value \(k^{hN}\) is the hadron momentum in the hadron-nucleon coordinate system.

The important difference of these calculations from the usual ones is that the two-gaussian form of the nuclear density was used

(224)\[\rho(r) = C \left( e^{-(r/R_{1})^2}-pe^{-(r/R_2)^2} \right),\]

where \(R_1\) \(R_2\) and \(p\) are the fitting parameters and \(C\) is a normalization constant.

This density representation allows the expressions for amplitude and differential cross section to be put into analytical form. It was earlier used for light [BW68, BDK+81, Cho68, NGG+78] and medium [EKS81, KS83] nuclei. Described below is an extension of this method to heavy nuclei. The form (224) is not physical for a heavy nucleus, but nevertheless works rather well (see figures below). The reason is that the nucleus absorbs the hadrons very strongly, especially at small impact parameters where the absorption is full. As a result only the peripherial part of the nucleus participates in elastic scattering. Eq. (224) therefore describes only the edge of a heavy nucleus.

Substituting Eqs. (224) and (223) into Eqs. (220), (221) and (222) yields the following formula

(225)\[\begin{split}F(q) &= \frac{ik\pi}{2} \sum\limits_{k=1}^A (-1)^k {A\choose k} [\frac{\sigma^{hN}}{2\pi(R_1^3-pR_2^3)}]^k \sum\limits_{m=0}^{k} (-1)^m {k \choose m} \left[ \frac{R_1^3}{R_1^2+2B} \right]^{k-m} \\ & \times \qquad {} \left[ \frac{pR_2^3}{R_2^2+2B} \right]^{m} \left( \frac{m}{R_2^2+2B}+\frac{k-m}{R_1^2+2B} \right)^{-1} \times \qquad {} \exp\left[ -\frac{-q^2}{4} \left( \frac{m}{R_2^2+2B}+ \frac{k-m}{R_1^2+2B} \right)^{-1} \right].\end{split}\]

An analogous procedure can be used to get the inelastic screening corrections to the hadron-nucleus amplitude \(\Delta M(\vec b)\) [NNikolskiiS+77]. In this case an intermediate inelastic diffractive state is created which rescatters on the nucleons of the nucleus and then returns into the initial hadron. Hence it is nessesary to integrate the production cross section over the mass distribution of the excited system \(d\sigma^{diff}/dtdM_x^2\). The expressions for the corresponding amplitude are quite long and so are not presented here. The corrections for the total cross-sections can be found in [NNikolskiiS+77].

The full amplitude is the sum \(M(\vec b)+ \Delta M(\vec b)\).

The differential cross section is connected with the amplitude in the following way

(226)\[\frac{d\sigma}{d\Omega_{CM}}=\left| F(q) \right|^2, \qquad \frac{d\sigma}{|dt|}=\frac{d\sigma}{dq_{CM}^2}= \frac{\pi}{k_{CM}^2} \left|F(q) \right|^2.\]

The main energy dependence of the hadron-nucleus elastic scattering cross section comes from the energy dependence of the parameters of hadron-nucleon scattering (\(\sigma_{tot}^{hN} \alpha\) \(B\) and \(\frac{d\sigma^{diff}}{dtdM_x^2}\)). At interesting energies these parameters were fixed at their well-known values. The fitting of the nuclear density parameters was performed over a wide range of atomic numbers \((A=4 - 208)\) using experimental data on proton-nuclei elastic scattering at a kinetic energy of \(T_p=1\) GeV.

The fitting was perfomed both for individual nuclei and for the entire set of nuclei at once. It is necessary to note that for every nucleus an optimal set of density parameters exists and it differs slightly from the one derived for the full set of nuclei.

A comparision of the phenomenological cross sections [ABV78] with experiment is presented in Fig. 66 - Fig. 74.

In this comparison, the individual nuclei parameters were used. The experimental data were obtained in Gatchina (Russia) and in Saclay (France) [ABV78]. The horizontal axis is the scattering angle in the center of mass system \(\Theta_{CM}\) and the vertical axis is \(\frac{\displaystyle d\sigma}{\displaystyle d\Omega_{CM}}\) in mb/Ster. Comparisions were also made for p4He elastic scatering at \(T = 1\) GeV [7], 45 GeV and 301 GeV [3]. The resulting cross sections \(\frac {d \sigma}{d\left| t \right|}\) are shown in Fig. 75 - Fig. 77.

In order to generate events the distribution function \({\cal F}\) of a corresponding process must be known. The differential cross section is proportional to the density distribution. Therefore to get the distribution function it is sufficient to integrate the differential cross section and normalize it:

(227)\[{\cal F}(q^2)= \frac {\displaystyle \int\limits_{0}^{q^2}d(q^2) \frac {\displaystyle d\sigma}{\displaystyle d(q^2)} } {\displaystyle \int\limits_{0}^{q_{max}^2}d(q^2) \frac {\displaystyle d\sigma}{\displaystyle d(q^2)} . }\]

Expressions (225) and (226) allow analytic integration in Eq. (227) but the result is too long to be given here.

For light and medium nuclei the analytic expression is more convenient for calculations than the numerical integration of Eq. (227), but for heavy nuclei the latter is preferred due to the large number of terms in the analytic expression.

../../_images/p_Be9_1.png

Fig. 66 Elastic proton scattering on 9Be at 1 GeV.

../../_images/p_B11_1.png

Fig. 67 Elastic proton scattering on 11B at 1 GeV.

../../_images/p_C12_1.png

Fig. 68 Elastic proton scattering on 12C at 1 GeV.

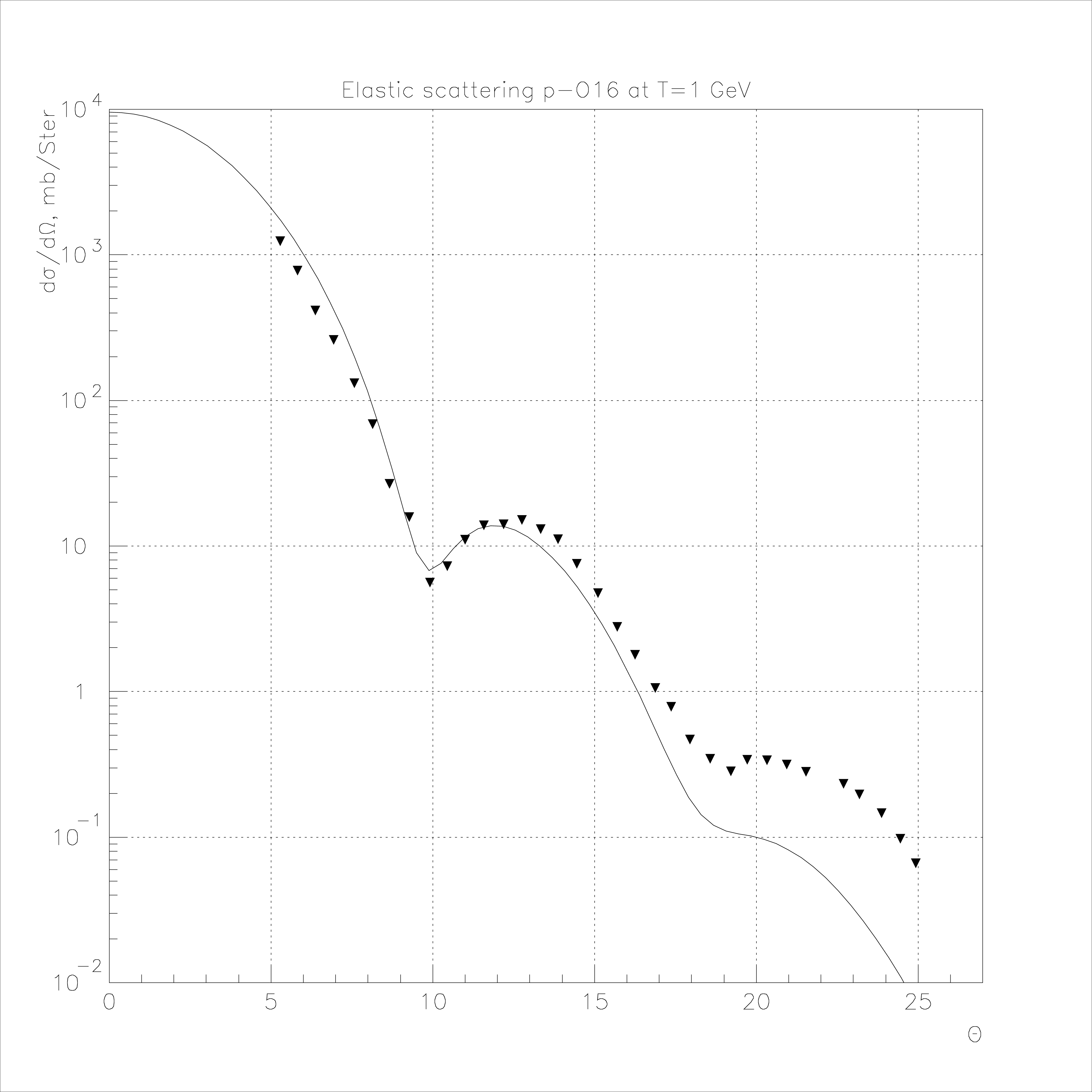
../../_images/p_016_1.png

Fig. 69 Elastic proton scattering on 16O at 1 GeV.

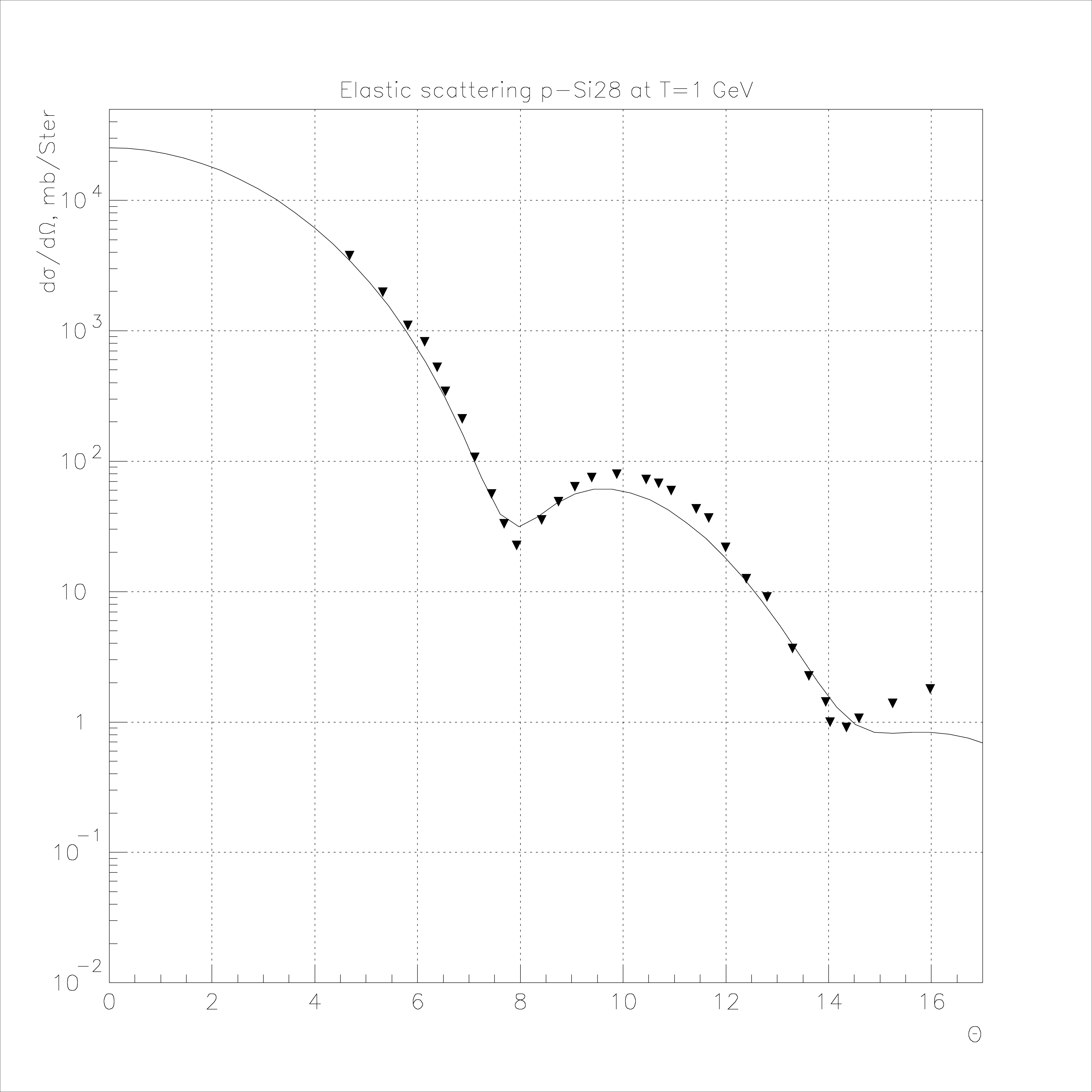
../../_images/p_Si28_1.png

Fig. 70 Elastic proton scattering on 28Si at 1 GeV.

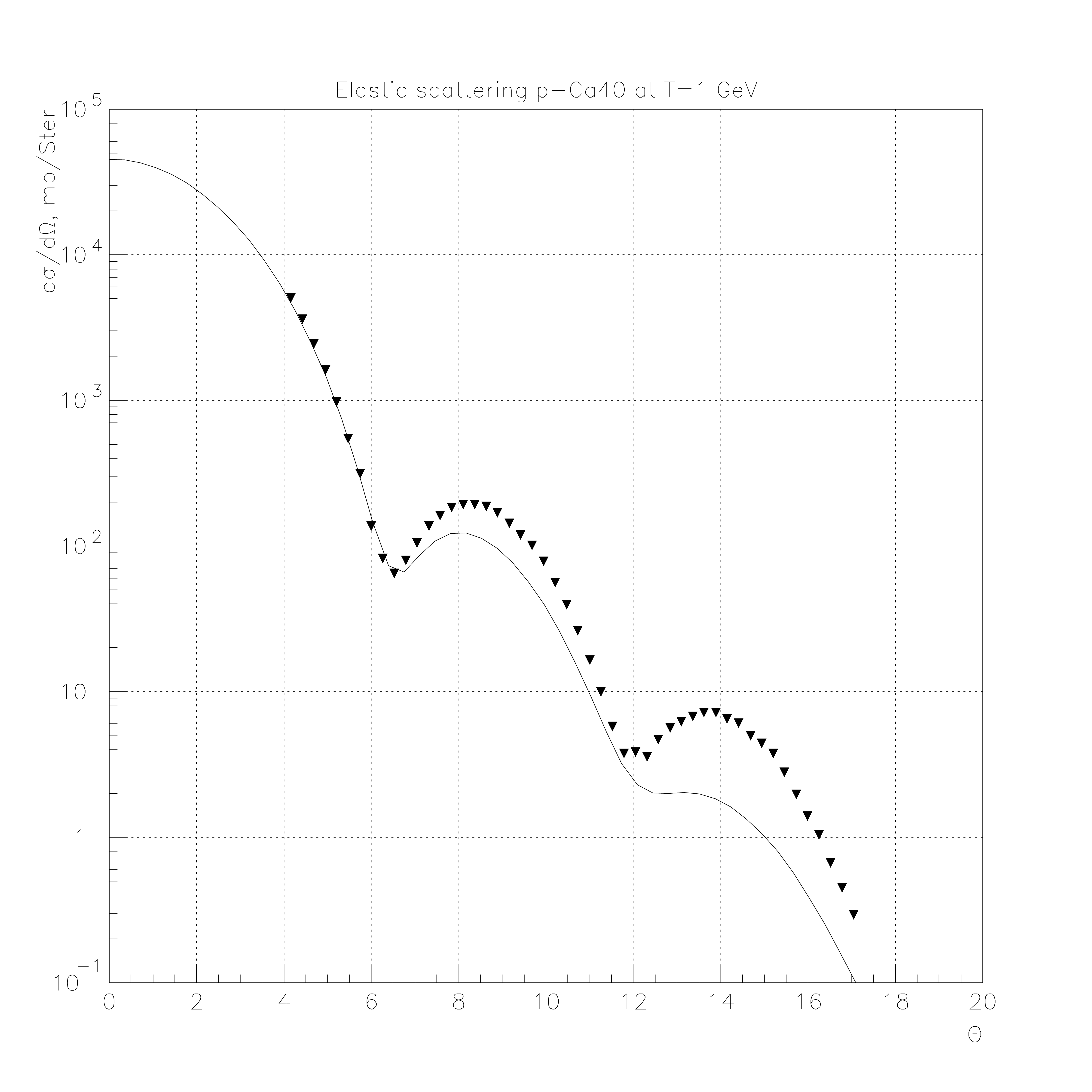
../../_images/p_Ca40_1.png

Fig. 71 Elastic proton scattering on 40Ca at 1 GeV.

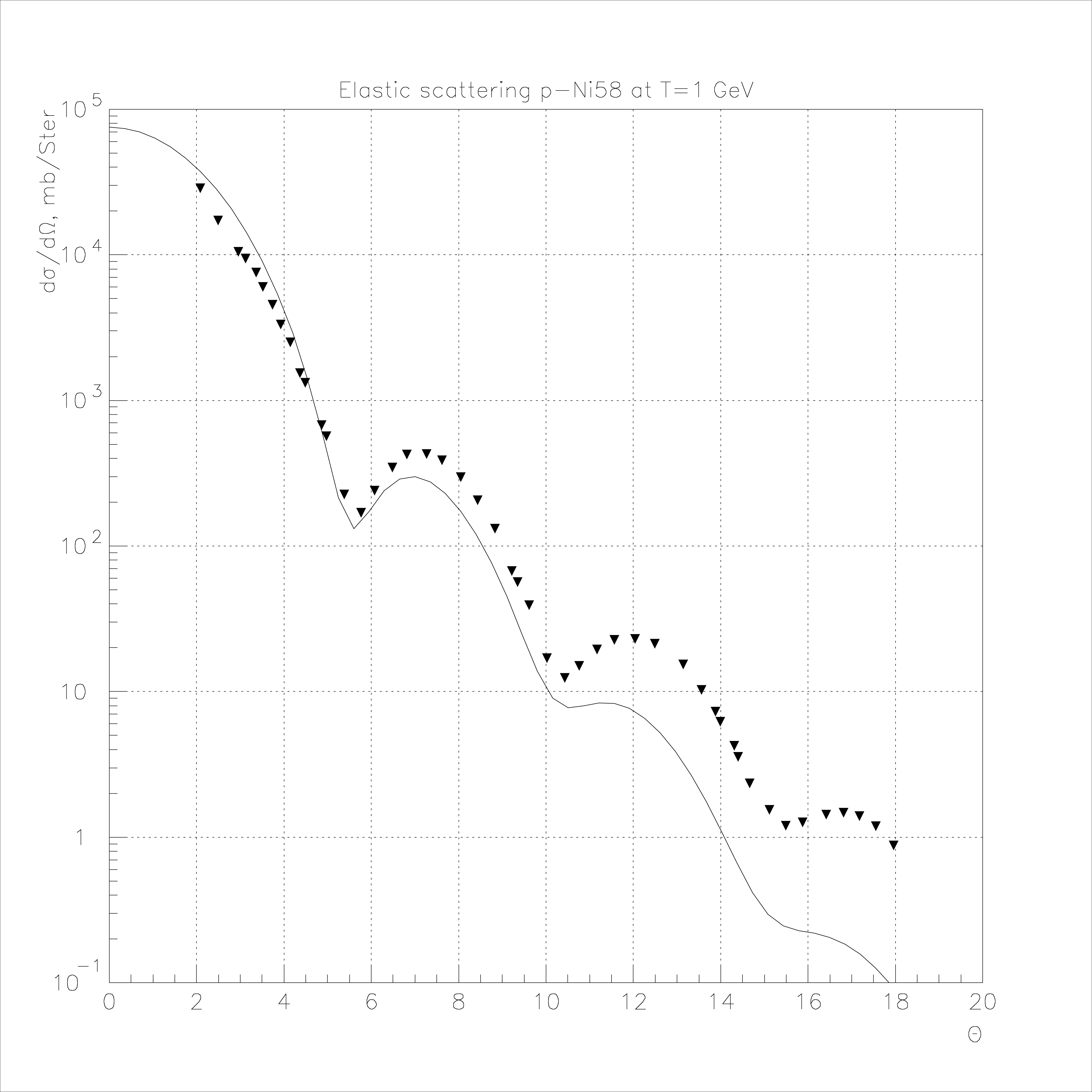
../../_images/p_Ni58_1.png

Fig. 72 Elastic proton scattering on 58Ni at 1 GeV.

../../_images/p_Zr90_1.png

Fig. 73 Elastic proton scattering on 90Zr at 1 GeV.

../../_images/p_Pb208_1.png

Fig. 74 Elastic proton scattering on 208Pb at 1 GeV.

../../_images/p_He4_1.png

Fig. 75 Elastic proton scattering on 4He at 1 GeV.

../../_images/p_He4_45.png

Fig. 76 Elastic proton scattering on 4He at 45 GeV.

../../_images/p_He4_301.png

Fig. 77 Elastic proton scattering on 4He at 301 GeV.

Bibliography

ABV78(1,2)

G.D. Alkhazov, S.L. Belostotsky, and A.A. Vorobyov. Scattering of 1 GeV protons on nuclei. Physics Reports, 42(2):89–144, Jun 1978. URL: https://doi.org/10.1016/0370-1573(78)90083-2, doi:10.1016/0370-1573(78)90083-2.

BW68

Robert H. Bassel and Colin Wilkin. High-energy proton scattering and the structure of light nuclei. Physical Review, 174(4):1179–1199, Oct 1968. URL: https://doi.org/10.1103/PhysRev.174.1179, doi:10.1103/physrev.174.1179.

BDK+81

A. Bujak, P. Devensky, A. Kuznetsov, B. Morozov, V. Nikitin, P. Nomokonov, Yu. Pilipenko, V. Smirnov, E. Jenkins, E. Malamud, M. Miyajima, and R. Yamada. Proton-helium elastic scattering from 45 to 400 GeV. Physical Review D, 23(9):1895–1910, May 1981. URL: https://doi.org/10.1103/PhysRevD.23.1895, doi:10.1103/physrevd.23.1895.

Cho68

T. T. Chou. Remarks on particle-nucleus scattering. Physical Review, 168(5):1594–1597, Apr 1968. URL: https://doi.org/10.1103/PhysRev.168.1594, doi:10.1103/physrev.168.1594.

EKS81

NT ERMEKOV, VL KOROTKIKH, and NI STARKOV. Estimate of the contribution of excitation of the 2+(1.78 mev) level of silicon to the cross-section for the reaction si-28(pi, 3-pi)si-28'. Soviet Journal of Nuclear Physics, 33(6):775–777, 1981.

Gla70

R.J. Glauber. High Energy Physics and Nuclear Structure. Plenum Press, NY, edited by s. devons edition, 1970.

KS83

VL KOROTKIKH and NI STARKOV. Photoproduction of heavy vector-mesons on nuclei with excitation of a discrete level. Soviet Journal of Nuclear Physics, 37(4):610–613, 1983.

NNikolskiiS+77(1,2)

R.A. Nam, S.I. Nikol’skii, N.I. Starkov, V.A. Tsarev, A.P. Chubenko, and V.I. Yakovlev. Proton-proton total cross sections from cosmic ray data. Sov. J. Nucl. Phys. (Engl. Transl.); (United States), 26:5:550–555, Nov 1977. Yad. Fiz. 26 1038 - Russian.

NGG+78

M.A. Nasser, M.M. Gazzaly, J.V. Geaga, B. Höistad, G. Igo, J.B. McClelland, A.L. Sagle, H. Spinka, J.B. Carroll, V. Perez-Mendez, and E.T.B. Whipple. P-4he elastic scattering at 2.68 GeV. Nuclear Physics A, 312(3):209–216, Dec 1978. URL: https://doi.org/10.1016/0375-9474(78)90586-9, doi:10.1016/0375-9474(78)90586-9.