Monash University Low Energy Model

Introduction

The Monash Compton Scattering models, for polarised (G4LowEPPolarizedComptonModel) and non-polarised (G4LowEPComptonModel) photons, are an alternative set of Compton scattering models to those of Livermore and Penelope that were constructed using Ribberfors’ theoretical framework [eal96, Kip04, Rib75]. The limitation of the Livermore and Penelope models is that only the components of the pre-collision momentum of the target electron contained within the photon plane, two-dimensional plane defined by the incident and scattered photon, is incorporated into their scattering frameworks [eal01]. Both models are forced to constrain the ejected direction of the Compton electron into the photon plane as a result. The Monash Compton scattering models avoid this limitation through the use of a two-body fully relativistic three-dimensional scattering framework to ensure the conservation of energy and momentum in the Relativistic Impulse Approximation (RIA) [eal14, Mon29].

Physics and Simulation

Total Cross Section

The Monash Compton scattering models were built using the Livermore and Polarised Livermore Compton scattering models as templates. As a result the total cross section for the Compton scattering process and handling of polarisation effects mimic those outlined in Low Energy Livermore Model.

Sampling of the Final State

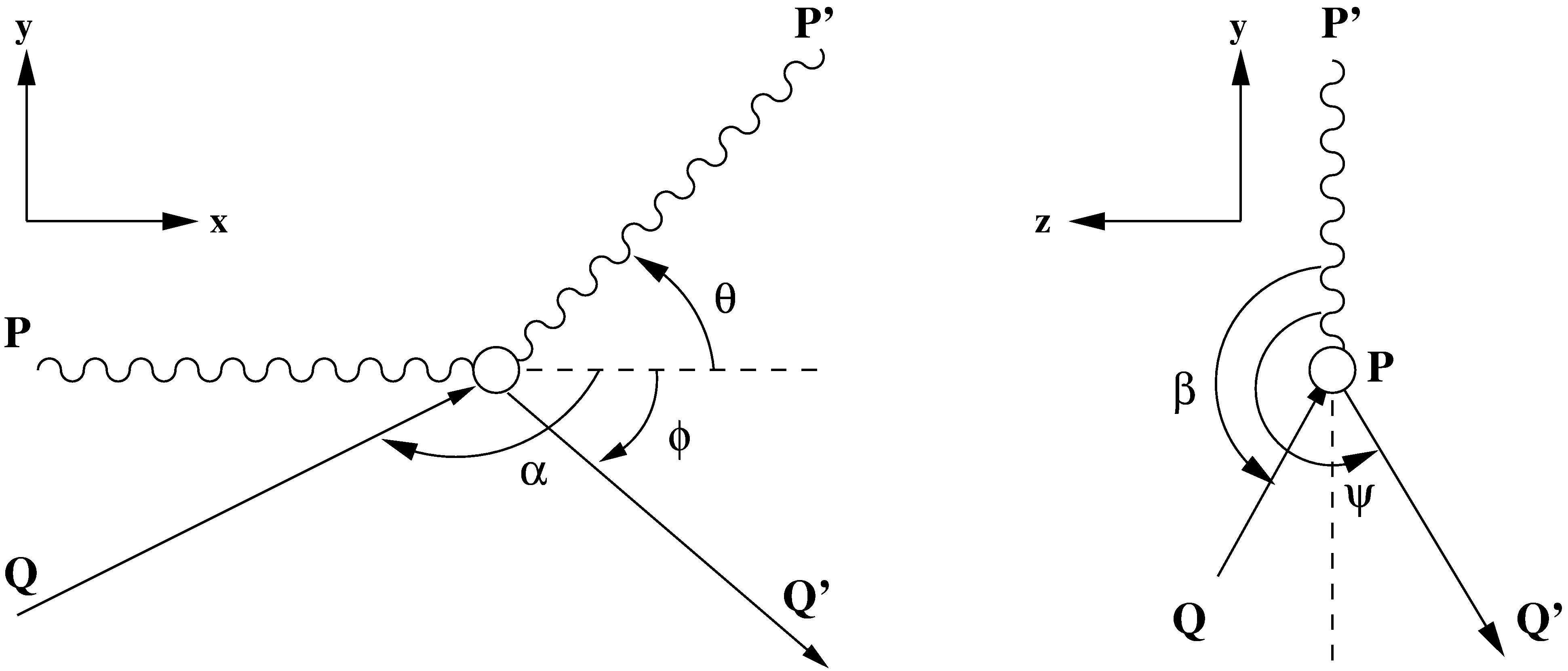
Fig. 2 Scattering diagram of atomic bound electron Compton scattering. \(\mathbf P\) is the incident photon momentum, \(\mathbf Q\) the electron pre-collision momentum, \(\mathbf P'\) the scattered photon momentum and \(\mathbf Q'\) the recoil electron momentum.

The scattering diagram seen in Fig. 2 outlines the basic principles of Compton scattering with an electron of non-zero pre-collision momentum in the RIA.

The process of sampling the target atom, atomic shell and target electron pre-collision momentum mimic that outlined in Low Energy Livermore Model. After the sampling of these parameters the following four equations are utilised to model the scattered photon energy \(E'\), recoil electron energy \(T_{el}\) and recoil electron polar and azimuthal angles (\(\phi\) and \(\psi\)) with respect to the incident photon direction and out-going plane of polarisation:

\[E'=\frac{\gamma mc\left(c - u\cos\alpha\right)}{1-\cos\theta+\frac{\gamma mc\left(c - u\cos\theta\cos\alpha - u\sin\theta\sin\alpha\cos\beta\right)}{E}},\]

\[T_{el} = E -E' - E_{B},\]

\[\cos\phi = \frac{-Y\pm \sqrt{Y^{2}-4WZ}}{2W},\]

\[\cos\psi = \frac{C-B\cos\phi}{A\sin\phi},\]

where:

\[A = E'u'\sin\theta,\]

\[B = E'u'\cos\theta-E u',\]

\[C = c\left(E' -E\right) - \frac{E E'}{\gamma' m c}\left(1 - \cos\theta\right),\]

\[ D = \frac{\gamma m E '}{c} \left(c - u\cos\theta\cos\alpha - u\sin\theta\cos\beta\sin\alpha\right) +m^{2}c^{2}\left(\gamma\gamma' -1\right) - \gamma'mE',\]

\[F = \left(\gamma\gamma'm^{2}uu'\cos\beta\sin\alpha - \frac{\gamma'mE'u'}{c}\sin\theta\right),\]

\[G = \gamma\gamma'm^{2}uu'\sin\beta\sin\alpha,\]

\[H = \left( \gamma\gamma'm^{2}uu'\cos\alpha - \frac{\gamma'mE'}{c}u'\cos\theta \right),\]

\[W=\left(FB-HA\right)^{2}+G^{2}A^{2}+G^{2}B^{2},\]

\[Y=2\left(\left(AD-FC\right)\left(FB-HA\right)-G^{2}BC\right),\]

\[Z=\left(AD-FC\right)^{2}+G^{2}\left(C^{2}-A^{2}\right),\]

and \(c\) is the speed of light, \(m\) is the rest mass of an electron, \(u\) is the speed of the target electron, \(u'\) is the speed of the recoil electron, \(\gamma =\left(1-\left(u^{2}/c^{2}\right)\right)^{-1/2}\) and \(\gamma' = \left(1-\left(u'^{2}/c^{2}\right)\right)^{-1/2}\). Further information regarding the Monash Compton scattering models can be found in [eal14].

Bibliography

eal96

D. Brusa et al. Nucl. Instrum. Methods Phys. Res. A, 379():167–175, 1996.

eal01

F. Salvat et al. Penelope, a code system for monte carlo simulation of electron and photon transport. Technical Report Proceedings of a Workshop/Training Course, OECD/NEA, 5-7 November 2001.

eal14(1,2)

J.M.C. Brown et al. Nucl. Instrum. Methods Phys. Res. B, 338():77–88, 2014.

Kip04

R.M. Kippen. New Astro. Reviews, 48():221–225, 2004.

Mon29

J.W.M. Du Mond. Phys. Rev., 33():643–658, 1929.

Rib75

R. Ribberfors. Phys. Rev. B., 12():2067–2074, 1975.